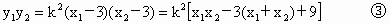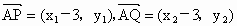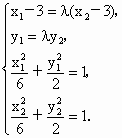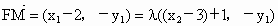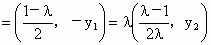题目内容
(2004
天津,22)椭圆的中心是原点O,它的短轴长是 ,相应于焦点F(c,0)(c>0)的准线l与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
,相应于焦点F(c,0)(c>0)的准线l与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
(1)
求椭圆的方程及离心率;(2)
若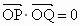 ,求直线PQ的方程;
,求直线PQ的方程;
(3)
设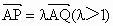 ,过点P且平行于准线l的直线与椭圆相交于另一点M,证明:
,过点P且平行于准线l的直线与椭圆相交于另一点M,证明: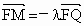 .
.
答案:略
解析:
解析:
|
解析: (1)由题意,可设椭圆的方程为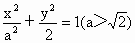 , ,
由已知得 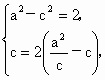
解得 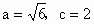 . .
所以椭圆的方程为 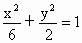 ,离心率 ,离心率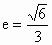 . .
(2) 由(1)可得A(3,0),设直线PQ的方程为y=k(x-3),由方程组 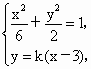 得 得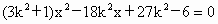 . .
依题意 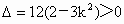 ,得 ,得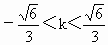 . .
设 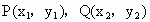 , ,
则 
由直线 PQ的方程得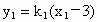 , ,
∵ 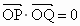 , ,
∴ 
由①②③④得 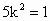 ,从而 ,从而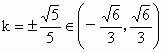 . .
所以直线 PQ的方程为 或 或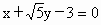 . .
(3)
注意 λ>1,解得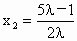 .因F(2,0), .因F(2,0),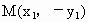 ,故 ,故
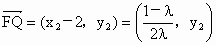 ,所以 ,所以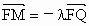 . . |

练习册系列答案
相关题目

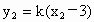 .
.