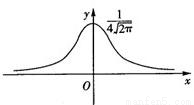
题目内容
标准正态分布的概率密度函数是P(x)=![]() ·
·![]() (x∈R).
(x∈R).
(1)求证:P(x)是偶函数;
(2)求P(x)的最大值;
(3)利用指数函数的性质说明P(x)的增减性.
(1)证明略(2)![]() (3)当x<0时,P(x)递增.当x>0时,P(x)递减.
(3)当x<0时,P(x)递增.当x>0时,P(x)递减.
解析:
(1)证明 对任意x∈R,有P(-x)= ![]()
![]()
=![]()
![]() =P(x),∴P(x)为偶函数.
=P(x),∴P(x)为偶函数.
(2)解 令t=![]() ,当x=0时,t=0,et=1.
,当x=0时,t=0,et=1.
∵et是关于t的增函数,当x≠0时,t>0,et>1.
∴当x=0,即t=0时,![]() =et取最小值.
=et取最小值.
∴当x=0时,P(x)=![]()
![]() 取得最大值
取得最大值![]() .
.
(3)解 任取x1<0,x2<0,且x1<x2,
有![]() >
>![]() ,∴
,∴![]() <
<![]() .
.
∴P(x1)<P(x2),即当x<0时,P(x)递增.
又P(x)为偶函数,由偶函数性质得,当x>0时,P(x)递减.

练习册系列答案
相关题目
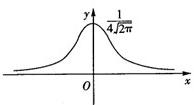 已知某正态分布的概率密度曲线f(x)=
已知某正态分布的概率密度曲线f(x)=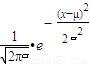 ,x∈(-∞,+∞)的图象如图,则函数的解析式为f(x)= .
,x∈(-∞,+∞)的图象如图,则函数的解析式为f(x)= .