题目内容
正方体的一条对角线与正方体的棱可组成n对异面直线，则n等于（ ）
分析：画图分析得到正方体的每一条对角线经过2个顶点，与6条棱相交，另外的6条棱中的若有棱与该对角线平行，则该对角线与相交棱中的一些棱也平行，得到矛盾，从而得到正方体的一条体对角线与正方体的棱可以组成异面直线的对数．
解答：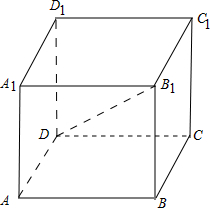
解：如图，
正方体的每一条对角线经过2个顶点，与6条棱相交，
而正方体的棱一共有12条，所以与正方体的棱可组成异面直线的对数是6对．
故选C．
解：如图，正方体的每一条对角线经过2个顶点，与6条棱相交，
而正方体的棱一共有12条，所以与正方体的棱可组成异面直线的对数是6对．
故选C．
点评：本题考查了异面直线的判定，考查了学生的空间想象能力和思维能力，是基础题．
练习册系列答案
阅读快车系列答案
相关题目