题目内容
函数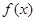 的定义域为
的定义域为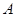 ,若
,若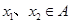 且
且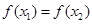 时总有
时总有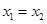 ,则称
,则称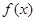 为单函数.例如,函数
为单函数.例如,函数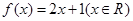 是单函数.下列命题:
是单函数.下列命题:
①若函数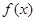 是
是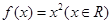 ,则
,则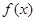 一定是单函数;
一定是单函数;
②若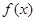 为单函数,
为单函数,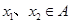 且
且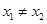 ,则
,则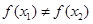 ;
;
③若定义在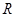 上的函数
上的函数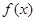 在某区间上具有单调性,则
在某区间上具有单调性,则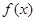 一定是单函数;
一定是单函数;
④若函数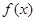 是周期函数,则
是周期函数,则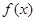 一定不是单函数;
一定不是单函数;
⑤若函数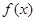 是奇函数,则
是奇函数,则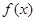 一定是单函数.
一定是单函数.
其中的真命题的序号是_______________.
【答案】
②④
【解析】
试题分析:因为,若x1,x2∈A,且f(x1)=f(x2)时总有x1=x2,则称f(x)为单函数。
① 函数f(x)=x2不是单函数,因为,f(-1)=f(1),显然-1≠1,
所以函数f(x)=x2(x∈R)不是单函数;
② 因为,函数f(x)是单函数,所以,f(x1)=f(x2)时总有x1=x2,即 且
且 ,则
,则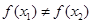 ,②正确;
,②正确;
③ 因为,如函数f(x)=x2在(0,+∞)上是增函数,而它不是单函数,即③不正确;
④ 由周期函数的定义,知,④若函数 是周期函数,则
是周期函数,则 一定不是单函数正确;
一定不是单函数正确;
⑤ 若函数 是奇函数,则
是奇函数,则 一定是单函数,不正确,如函数,y=sinx是奇函数,显然不是的函数。
一定是单函数,不正确,如函数,y=sinx是奇函数,显然不是的函数。
综上知,答案为②④。
考点:本题主要考查新定义“单函数”的概念。
点评:简单题,关键是理解新定义,注意严格审题,如“定义在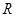 上的函数
上的函数 在某区间上具有单调性”与“在定义域上具有单调性”,而这时不同的。
在某区间上具有单调性”与“在定义域上具有单调性”,而这时不同的。

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
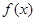 的定义域为
的定义域为 ,若
,若 且
且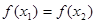 时总有
时总有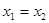 ,则称
,则称 是单函数.下列命题:
是单函数.下列命题: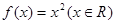 是单函数;
是单函数;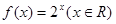 是单函数;
是单函数;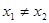 ,则
,则 ;
;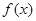 的定义域为
的定义域为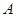 ,若
,若 且
且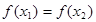 时总有
时总有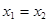 ,则称
,则称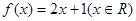 是单函数.下列命题:
是单函数.下列命题: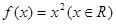 是单函数;
是单函数; 是单函数;
是单函数; ,则
,则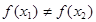 ;
;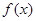 的定义域为
的定义域为 ,若
,若 且
且 时总有
时总有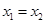 ,则称
,则称 是单函数.下列命题:
是单函数.下列命题: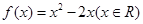 是单函数;
是单函数; 是单函数;
是单函数;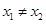 ,则
,则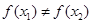 ;
; 在定义域内某个区间
在定义域内某个区间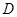 上具有单调性,则
上具有单调性,则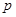 :函数
:函数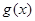 =
= 是
是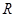 上的减函数,命题
上的减函数,命题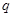 :函数
:函数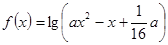 的定义域为
的定义域为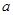 的取值范围.
的取值范围. 的定义域为
的定义域为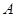 ,若
,若 且
且 时总有
时总有 ,则称
,则称
 是单函数。下列命题:
是单函数。下列命题:
 是单函数;
是单函数;
 ,则
,则 ;
;