题目内容
不等式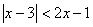 的解集是 .
的解集是 .
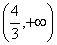
解析试题分析:解含绝对值的不等式可以分类讨论,当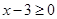 即
即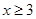 时,不等式变为
时,不等式变为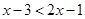 得
得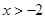 ,因此
,因此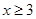 ;当
;当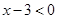 即
即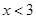 时,不等式变为
时,不等式变为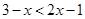 得
得 ,因此
,因此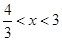 ,所以原不等式的解是把所得两个集合合并得
,所以原不等式的解是把所得两个集合合并得 .
.
考点:解含绝对值的不等式.

练习册系列答案
相关题目
题目内容
不等式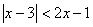 的解集是 .
的解集是 .
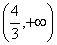
解析试题分析:解含绝对值的不等式可以分类讨论,当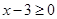 即
即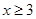 时,不等式变为
时,不等式变为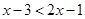 得
得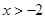 ,因此
,因此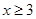 ;当
;当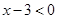 即
即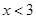 时,不等式变为
时,不等式变为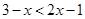 得
得 ,因此
,因此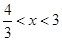 ,所以原不等式的解是把所得两个集合合并得
,所以原不等式的解是把所得两个集合合并得 .
.
考点:解含绝对值的不等式.
