题目内容
由于浓酸泄漏对河流形成了污染,现决定向河中投入固体碱.1个单位的固体碱在水中逐步溶化,水中的碱浓度y与时间x的关系,可近似地表示为y=
.只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用.
(1)如果只投放1个单位的固体碱,则能够维持有效抑制作用的时间有多长?
(2)当河中的碱浓度开始下降时,即刻第二次投放1个单位的固体碱,此后,每一时刻河中的碱浓度认为是各次投放的碱在该时刻相应的碱浓度的和,求河中碱浓度可能取得的最大值.
|
(1)如果只投放1个单位的固体碱,则能够维持有效抑制作用的时间有多长?
(2)当河中的碱浓度开始下降时,即刻第二次投放1个单位的固体碱,此后,每一时刻河中的碱浓度认为是各次投放的碱在该时刻相应的碱浓度的和,求河中碱浓度可能取得的最大值.
分析:(1)利用分段函数解析式,分别列出不等式,解之,即可求得x的范围,从而可得能够维持有效抑制作用的时间;
(2)确定函数y=-
-x+8在[0,2]上单调递增,当2<x≤4时,y=4-x单调递减,进而可得函数,利用基本不等式,即可求得最值
(2)确定函数y=-
| 16 |
| x+2 |
解答:解:(1)由题意,当0≤x≤2时,-
-x+8≥1,∴x2-5x+2≤0,∴
≤x≤
,
∵0≤x≤2,∴
≤x≤2
当2<x≤4时,4-x≥1,∴x≤3,∵2<x≤4,∴2<x≤3
综上,得
≤x≤3,
即若1个单位的固体碱只投放一次,则能够维持有效抑制作用的时间为3-
=
;
(2)当0≤x≤2时,y=-
-x+8,y′=
-1>0,∴函数y=-
-x+8在[0,2]上单调递增,
当2<x≤4时,y=4-x单调递减,所以当河中的碱浓度开始下降时,即刻第二次投放1个单位的固体碱,
即2<x≤4时,y=4-x+[-
-(x-2)+8]=14-(2x+
),
故当且仅当2x=
,即x=2
时,y有最大值14-8
.
| 16 |
| x+2 |
5-
| ||
| 2 |
5+
| ||
| 2 |
∵0≤x≤2,∴
5-
| ||
| 2 |
当2<x≤4时,4-x≥1,∴x≤3,∵2<x≤4,∴2<x≤3
综上,得
5-
| ||
| 2 |
即若1个单位的固体碱只投放一次,则能够维持有效抑制作用的时间为3-
5-
| ||
| 2 |
1+
| ||
| 2 |
(2)当0≤x≤2时,y=-
| 16 |
| x+2 |
| 16 |
| (x+2)2 |
| 16 |
| x+2 |
当2<x≤4时,y=4-x单调递减,所以当河中的碱浓度开始下降时,即刻第二次投放1个单位的固体碱,
即2<x≤4时,y=4-x+[-
| 16 |
| (x-2)+2 |
| 16 |
| x |
故当且仅当2x=
| 16 |
| x |
| 2 |
| 2 |
点评:本题考查分段函数,考查解不等式,考查函数的单调性,考查利用基本不等式求函数的最值,确定函数的解析式是关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
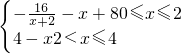 .只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用.
.只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用. .只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用.
.只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用. 与时间
与时间 的关系,可近似地表示为
的关系,可近似地表示为 。只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用。
。只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用。