题目内容
已知函数f(x)= (a>1,x≥1)
(a>1,x≥1)
(Ⅰ)求它的反函数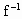 (x),并指出
(x),并指出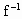 (x)的定义域;
(x)的定义域;
(Ⅱ)当1<a<2时,证明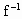 (n)<
(n)< (n∈
(n∈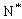 )
)
答案:
解析:
解析:
|
(1)x+
解得 x= ∵x≥1,∴x+ ∵a>1,∴f(x)= 故 (2)证明:
∵1<a<2,∴ 则 故 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 -x.
-x.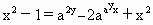
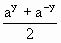 ,∴
,∴ (x)=
(x)=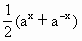 .
.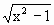 ≥1.
≥1.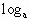 (x+
(x+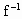 (x)=
(x)=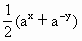 x∈[0,+∞).
x∈[0,+∞).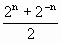 =
= (
(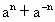 )-
)-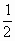 (
( )
)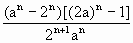
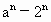 <0,
<0, -1>0,
-1>0,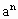 >0,
>0, <0.即,
<0.即,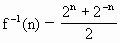 <0
<0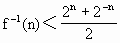 (n∈N).
(n∈N).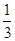 )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有