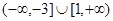题目内容
已知抛物线 上一定点B(-1,0)和两个动点
上一定点B(-1,0)和两个动点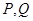 ,当
,当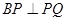 时,点
时,点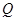 的横坐标的取值范围是
的横坐标的取值范围是
A.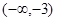 ∪
∪ 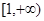 B.
B.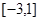
C.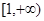 D.(-∞,-3]∪
D.(-∞,-3]∪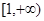
【答案】
D
【解析】
试题分析:设P(t,t2-1),Q(s,s2-1),∵BP⊥PQ,
∴ =-1,
=-1,
即t2+(s-1)t-s+1=0
∵t∈R,P,Q是抛物线上两个不同的点,∴必须有△=(s-1)2+4(s-1)≥0.
即s2+2s-3≥0,解得s≤-3或s≥1.
∴Q点的横坐标的取值范围是 (-∞,-3]∪[1,+∞),故选D。
考点:直线垂直的条件,直线与抛物线的位置关系。
点评:中档题,解题的关键是利用斜率之积为-1构建方程,再利用方程根的判别式大于等于0进行求解

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
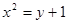 上一定点
上一定点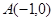 和两动点
和两动点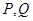 ,当
,当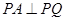 时,点
时,点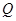 的横坐标的取值范围是( )
的横坐标的取值范围是( )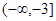 B.
B.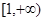 C.[
C.[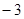 ,1] D.
,1] D.