题目内容
(本小题共16分)
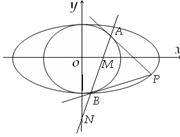
已知椭圆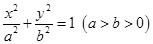 和圆
和圆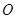 :
: ,过椭圆上一点
,过椭圆上一点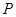 引圆
引圆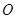 的两条切线,切点分别为
的两条切线,切点分别为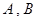 . (1)①若圆
. (1)①若圆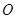 过椭圆的两个焦点,求椭圆的离心率
过椭圆的两个焦点,求椭圆的离心率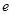 ; ②若椭圆上存在点
; ②若椭圆上存在点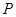 ,使得
,使得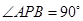 ,求椭圆离心率
,求椭圆离心率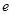 的取值(2)设直线
的取值(2)设直线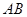 与
与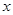 轴、
轴、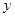 轴分别交于点
轴分别交于点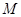 ,
,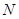 ,求证:
,求证: 为定值.
为定值.
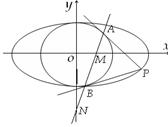
【答案】
(1)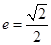 ,
,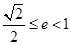
(2)略
【解析】解:(Ⅰ)(ⅰ)∵ 圆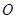 过椭圆的焦点,圆
过椭圆的焦点,圆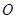 :
: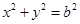 ,
,
∴ 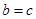 ,∴
,∴ 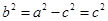 ,
,
∴ 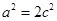 ,∴
,∴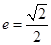 . ……… 5分
. ……… 5分
(ⅱ)由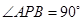 及圆的性质,可得
及圆的性质,可得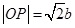 ,
,
∴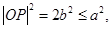 ∴
∴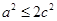
∴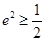 ,
,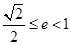 . ……… 10分
. ……… 10分
(Ⅱ)设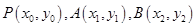 ,则
,则
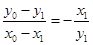 整理得
整理得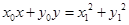
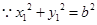 ∴
∴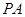 方程为:
方程为: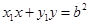 ,
,
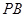 方程为:
方程为: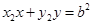 .∴
.∴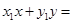
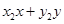 ,
,
∴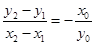 ,
,
直线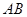 方程为
方程为 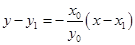 ,即
,即 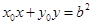 .
.
令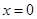 ,得
,得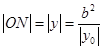 ,令
,令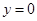 ,得
,得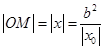 ,
,
∴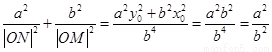 ,
,
∴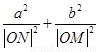 为定值,定值是
为定值,定值是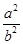 ……… 16分
……… 16分

练习册系列答案
相关题目
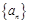 各项均不为0,其前
各项均不为0,其前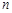 项和为
项和为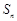 ,且对任意
,且对任意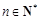 都有
都有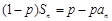 (
(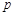 为大于1的常数),记f(n)
为大于1的常数),记f(n)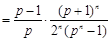 .
.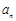 ;
;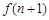 与
与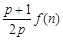 的大小(
的大小(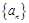 各项均不为0,其前
各项均不为0,其前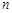 项和为
项和为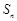 ,且对任意
,且对任意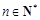 都有
都有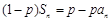 (
(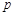 为大于1的常数),记f(n)
为大于1的常数),记f(n)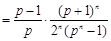 .
.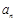 ;
;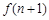 与
与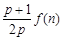 的大小(
的大小( 和圆
和圆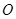 :
: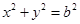 ,过椭圆上一点
,过椭圆上一点 引圆
引圆 .
. 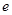 ; ②若椭圆上存在点
; ②若椭圆上存在点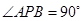 ,求椭圆离心率
,求椭圆离心率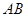 与
与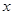 轴、
轴、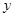 轴分别交于点
轴分别交于点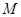 ,
,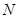 ,求证:
,求证: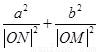 为定值.
为定值.