题目内容
已知 ,已知数列{an}满足0<an≤3,n∈N*,且a1+a2+…+a2010=670,则f(a1)+f(a2)+…+f(a2010)有( )
,已知数列{an}满足0<an≤3,n∈N*,且a1+a2+…+a2010=670,则f(a1)+f(a2)+…+f(a2010)有( )A.最大值6030
B.最大值6027
C.最小值6027
D.最小值6030
【答案】分析:由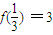 ,知当
,知当 时,f(a1)+f(a2)+…+f(a2010)=6030.对于函数
时,f(a1)+f(a2)+…+f(a2010)=6030.对于函数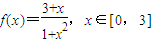 ,k=
,k=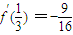 ,在
,在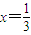 处的切线方程为
处的切线方程为 ,由此能导出f(a1)+f(a2)+…+f(a2010)≤
,由此能导出f(a1)+f(a2)+…+f(a2010)≤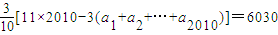 .
.
解答:解:∵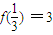 ,当
,当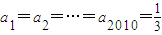 时,
时,
f(a1)+f(a2)+…+f(a2010)=6030,
对于函数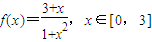 ,k=
,k=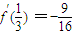 ,
,
在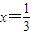 处的切线方程为
处的切线方程为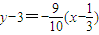 ,
,
即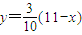 ,
,
则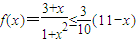 ?
?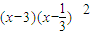 ≤0成立,
≤0成立,
∴0<an≤3,n∈N+时,有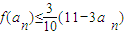 ,
,
∴f(a1)+f(a2)+…+f(a2010)≤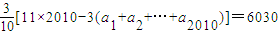 .
.
故选A.
点评:本题考查数列和函数的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地运用导数的性质,恰当地进行等价转化.
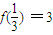 ,知当
,知当 时,f(a1)+f(a2)+…+f(a2010)=6030.对于函数
时,f(a1)+f(a2)+…+f(a2010)=6030.对于函数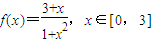 ,k=
,k=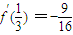 ,在
,在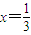 处的切线方程为
处的切线方程为 ,由此能导出f(a1)+f(a2)+…+f(a2010)≤
,由此能导出f(a1)+f(a2)+…+f(a2010)≤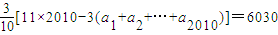 .
.解答:解:∵
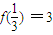 ,当
,当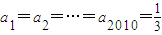 时,
时,f(a1)+f(a2)+…+f(a2010)=6030,
对于函数
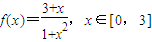 ,k=
,k=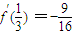 ,
,在
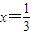 处的切线方程为
处的切线方程为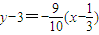 ,
,即
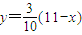 ,
,则
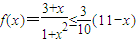 ?
?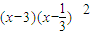 ≤0成立,
≤0成立,∴0<an≤3,n∈N+时,有
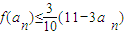 ,
,∴f(a1)+f(a2)+…+f(a2010)≤
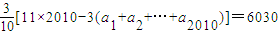 .
.故选A.
点评:本题考查数列和函数的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地运用导数的性质,恰当地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

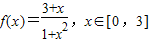 ,已知数列{an}满足0<an≤3,n∈N*,且a1+a2+…+a2010=670,则f(a1)+f(a2)+…+f(a2010)有( )
,已知数列{an}满足0<an≤3,n∈N*,且a1+a2+…+a2010=670,则f(a1)+f(a2)+…+f(a2010)有( )