题目内容
甲袋装有m个白球,n个黑球,乙袋装有n个白球,m个黑球,(m≠n),现从两袋中各摸一个球,A:“两球同色”,B:“两球异色”,求证:P(A)<P(B).
解:以A1表示取出的都是白球.A2表示取出的都是黑球,则
∵A1,A2互斥且A=A1∪A2,
∴P(A)=P(A1)+P(A2)=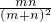 +
+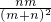 =
=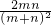 .
.
以B1表示甲袋取出白球乙袋取出黑球,B2表示甲袋取出黑球乙袋取出白球,
∵B1、B2互斥且B=B1∪B2,
∴P(B)=P(B1)+P(B2)=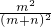 +
+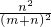 =
=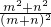 .
.
由于m≠n,故2mn<m2+n2.
∴P(A)<P(B).
分析:由题意知将A、B分别分解为互斥事件,利用互斥事件来表示要比较的两个事件的概率,根据等可能事件的概率写出P(A1)与P(A2),P(B1)与P(B2),利用互斥事件的概率表示出A与B的概率,根据基本不等式进行比较得到结果.
点评:由题意知本题也可以这样解:显然B= ,所以按解法一解出P(A)后,可得P(B)=1-P(A)=
,所以按解法一解出P(A)后,可得P(B)=1-P(A)=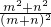 .比较P(A)、P(B)即可.
.比较P(A)、P(B)即可.
∵A1,A2互斥且A=A1∪A2,
∴P(A)=P(A1)+P(A2)=
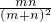 +
+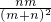 =
=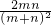 .
.以B1表示甲袋取出白球乙袋取出黑球,B2表示甲袋取出黑球乙袋取出白球,
∵B1、B2互斥且B=B1∪B2,
∴P(B)=P(B1)+P(B2)=
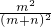 +
+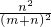 =
=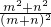 .
.由于m≠n,故2mn<m2+n2.
∴P(A)<P(B).
分析:由题意知将A、B分别分解为互斥事件,利用互斥事件来表示要比较的两个事件的概率,根据等可能事件的概率写出P(A1)与P(A2),P(B1)与P(B2),利用互斥事件的概率表示出A与B的概率,根据基本不等式进行比较得到结果.
点评:由题意知本题也可以这样解:显然B=
 ,所以按解法一解出P(A)后,可得P(B)=1-P(A)=
,所以按解法一解出P(A)后,可得P(B)=1-P(A)=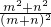 .比较P(A)、P(B)即可.
.比较P(A)、P(B)即可. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
甲袋装有m个白球,n个黑球,乙袋装有n个白球,m个黑球,(m≠n),现从两袋中各摸一个球,A:“两球同色”,B:“两球异色”,则P(A)与P(B)的大小关系为( )
| A、P(A)<P(B) | B、P(A)=P(B) | C、P(A)>P(B) | D、视m,n的大小而定 |