题目内容
某种家电器每台的销售利润与该电器无故障使用时间T(单位:年)有关,若T≤1,则销售利润为0元,若1<T≤3,则销售利润为100元,若T>3,则销售利润为200元,设每台该种电台无故障使用时间T≤1,1<T≤3及T>3这三种情况发生的概率为P1,P2,P3,又知P1,P2是方程25x2-15x+a=0的两个根,且P2=P3,(1)求P1,P2,P3的值;
(2)记ξ表示销售两台这种家用电器的销售利润总和,求ξ的分布列和期望
分析:(1)根据题目中所给的三种情况发生的概率P1,P2,P3之间的关系,写出关于三个概率的关系式,即三个概率之和是1,又两个概率是一元二次方程的解,根据根和系数之间的关系,写出结果.
(2)ξ表示销售两台这种家用电器的销售利润总和,则ξ的可能取值为0,100,200,300,400,结合变量对应的事件写出变量的分布列,做出数学期望.
(2)ξ表示销售两台这种家用电器的销售利润总和,则ξ的可能取值为0,100,200,300,400,结合变量对应的事件写出变量的分布列,做出数学期望.
解答:解:(1)由已知P1+P2+P3=1,
∵P2=P3,∴P1+2P2=1
∵P1,P2是方程25x2-15x+a=0的两个根,
∴P1+P2=
,∴P1=
,P2=P3=
(2)ξ的可能取值为0,100,200,300,400
P(ξ=0)=
×
=
P(ξ=100)=2×
×
=
P(ξ=200)=2×
×
+
×
=
P(ξ=300)=2×
×
=
P(ξ=400)=
×
=
∴随机变量ξ的分布列为:
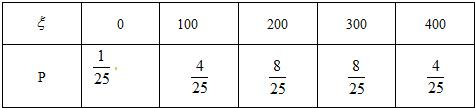
Eξ=0×
+100×
+200×
+300×
+400×
=240元
∵P2=P3,∴P1+2P2=1
∵P1,P2是方程25x2-15x+a=0的两个根,
∴P1+P2=
| 3 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
(2)ξ的可能取值为0,100,200,300,400
P(ξ=0)=
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 25 |
P(ξ=100)=2×
| 1 |
| 5 |
| 2 |
| 5 |
| 4 |
| 25 |
P(ξ=200)=2×
| 1 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 8 |
| 25 |
P(ξ=300)=2×
| 2 |
| 5 |
| 2 |
| 5 |
| 8 |
| 25 |
P(ξ=400)=
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
| 25 |
∴随机变量ξ的分布列为:

Eξ=0×
| 1 |
| 25 |
| 4 |
| 25 |
| 8 |
| 25 |
| 8 |
| 25 |
| 4 |
| 25 |
点评:本题考查离散型随机变量的分布列和期望,考查概率的性质,考查一元二次方程根和系数之间的关系,是一个综合题目.

练习册系列答案
相关题目
 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求