题目内容
已知一元二次方程7x2-(k+13)x-k+2=0的两根x1x2满足0<x1<1,1<x2<2,求k的取值范围.分析:由题意可得:设f(x)=7x2-(k+13)x-k+2,所以
,进而求出答案.
|
解答:解:设f(x)=7x2-(k+13)x-k+2方程的两根x1x2满足0<x1<1,1<x2<2,
∴
即
解得:-2<k<
,
所以k的取值范围是:-2<k<
.
∴
|
|
解得:-2<k<
| 4 |
| 3 |
所以k的取值范围是:-2<k<
| 4 |
| 3 |
点评:本题主要考查一元二次方程的根的分布,即考查实根分布问题,解决此类问题的关键是熟练掌握一元二次函数的图象.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
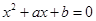 的一个根在-2与-1之间,另一个根在1与2之间,试求点
的一个根在-2与-1之间,另一个根在1与2之间,试求点 的轨迹及
的轨迹及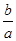 的范围.
的范围.