题目内容
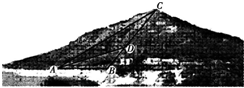
 如图所示,福建省福清石竹山原有一条笔直的山路BC,现在又新架设了一条索道AC.小明在山脚B处看索道AC,此时张角∠ABC=120°;从B处攀登200米到达D处,回头看索道AC,此时张角∠ADC=150°;从D处再攀登300米到达C处.问石竹山这条索道AC长多少米?
如图所示,福建省福清石竹山原有一条笔直的山路BC,现在又新架设了一条索道AC.小明在山脚B处看索道AC,此时张角∠ABC=120°;从B处攀登200米到达D处,回头看索道AC,此时张角∠ADC=150°;从D处再攀登300米到达C处.问石竹山这条索道AC长多少米?分析:在△ABC中根据∠ABD=120°,∠ADB=180°-∠ADC=30°,利用内角和定理算出∠DAB=30°,从而AB=BD=200,利用余弦定理算出AD=200
.然后在△ADC中,根据两边AD、DC长和夹角∠ADC=150°,利用余弦定理解出AC2=390000,从而得出AC=100
,即得石竹山这条索道AC的长.
| 3 |
| 39 |
解答: 解:在△ABD中,BD=200米,∠ABD=120°,
解:在△ABD中,BD=200米,∠ABD=120°,
∵∠ADB=180°-∠ADC=30°
∴∠DAB=180°-120°-30°=30°
得△ABD中,AB=BD=200,AD=
=200
(米)
在△ADC中,DC=300,∠ADC=150°
∴AC2=AD2+DC2-2 AD•DC•cos∠ADC
=2002×3+3002-2×200
×300×cos150°=390000(米2)
∴AC=
=100
(米)
答:石竹山这条索道AC长100
米.
 解:在△ABD中,BD=200米,∠ABD=120°,
解:在△ABD中,BD=200米,∠ABD=120°,∵∠ADB=180°-∠ADC=30°
∴∠DAB=180°-120°-30°=30°
得△ABD中,AB=BD=200,AD=
| AB2+BD2-2AD•BDcos120° |
| 3 |
在△ADC中,DC=300,∠ADC=150°
∴AC2=AD2+DC2-2 AD•DC•cos∠ADC
=2002×3+3002-2×200
| 3 |
∴AC=
| 390000 |
| 39 |
答:石竹山这条索道AC长100
| 39 |
点评:本题以山上的索道为例,求石竹山的一条索道AC之长.着重考查了三角形内角和定理、利用正余弦定理解三角形等知识,属于中档题.

练习册系列答案
相关题目