题目内容
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验.每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效.若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组.设每只小白鼠服用A有效的概率为| 2 |
| 3 |
| 1 |
| 2 |
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ) 观察3个试验组,用n表示这3个试验组中甲类组的个数,求n取不同值时的概率.
分析:(1)由题意知本题是一个独立重复试验,根据所给的两种药物对小白鼠有效的概率,计算出小白鼠有效的只数的概率,对两种药物有效的小白鼠进行比较,得到甲类组的概率.
(2)由题意知本试验是一个甲类组的概率不变,实验的条件不变,可以看做是一个独立重复试验,所以变量服从二项分布,根据二项分布的性质写出变量的概率.
(2)由题意知本试验是一个甲类组的概率不变,实验的条件不变,可以看做是一个独立重复试验,所以变量服从二项分布,根据二项分布的性质写出变量的概率.
解答:解:(1)设Ai表示事件“一个试验组中,服用A有效的小鼠有i只“,i=0,1,2,
Bi表示事件“一个试验组中,服用B有效的小鼠有i只“,i=0,1,2,
依题意有:P(A1)=2×
×
=
,P(A2)=
×
=
.P(B0)=
×
=
,
P(B1)=2×
×
=
,
所求概率为:P=P(B0•A1)+P(B0•A2)+P(B1•A2)=
×
+
×
+
×
=
(Ⅱ) n的可能值为0,1,2,3且n~B(3,
).
P(n=0)=(
)3=
,
P(n=1)=C31×
×(
)2=
P(n=2)=C32×(
)2×
=
,
P(n=3)=(
)3=
Bi表示事件“一个试验组中,服用B有效的小鼠有i只“,i=0,1,2,
依题意有:P(A1)=2×
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
P(B1)=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所求概率为:P=P(B0•A1)+P(B0•A2)+P(B1•A2)=
| 1 |
| 4 |
| 4 |
| 9 |
| 1 |
| 4 |
| 4 |
| 9 |
| 1 |
| 2 |
| 4 |
| 9 |
| 4 |
| 9 |
(Ⅱ) n的可能值为0,1,2,3且n~B(3,
| 4 |
| 9 |
P(n=0)=(
| 5 |
| 9 |
| 125 |
| 729 |
P(n=1)=C31×
| 4 |
| 9 |
| 5 |
| 9 |
| 100 |
| 243 |
P(n=2)=C32×(
| 4 |
| 9 |
| 5 |
| 9 |
| 80 |
| 243 |
P(n=3)=(
| 4 |
| 9 |
| 64 |
| 729 |
点评:本题考查相互独立事件的概率,这种类型是近几年高考题中经常出现的,结合考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道问题

练习册系列答案
相关题目
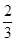 ,服用B有效的概率为
,服用B有效的概率为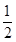 .
.