题目内容
如图, 是正方形ABCD的内接三角形,若
是正方形ABCD的内接三角形,若 ,则点C分线段BE所成的比为( ).
,则点C分线段BE所成的比为( ). 
A. | B. |
C. | D.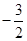 |
B
解析试题分析:设 ,
,
则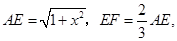
 ,
,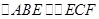 ,
,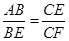 ,
, ,
,
解得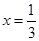 ,所以
,所以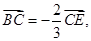
故选B。
考点:平面向量的应用
点评:简单题,平面向量在平面几何中的应用,一般借助于图形,发现向量之间的关系,利用向量的线性运算,加以解答。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设 、
、 都是非零向量,下列四个条件中,一定能使
都是非零向量,下列四个条件中,一定能使 成立的是( )
成立的是( )
A. | B. | C. | D. |
点 共面,若
共面,若 ,则
,则 的面积与
的面积与 的面积之比为( )
的面积之比为( )
A. | B. | C. | D. |
在 中,
中,  ,
, ,
, 为
为 的中点 ,则
的中点 ,则 =( )
=( )
| A.3 | B. | C.-3 | D. |
已知O是△ABC内一点,若 ,则△AOC与△ABC的面积的比值为 ( )
,则△AOC与△ABC的面积的比值为 ( )
A. | B. | C. | D. |
已知点G是ΔABC的重心, ,
,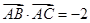 ,则
,则 的最小值是
的最小值是
A.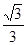 | B. | C. | D. |
设点P是△ABC所在平面内一点, ,则点P是△ABC
,则点P是△ABC
| A.内心 | B.外心 | C.重心 | D.垂心 |
已知非零向量a,b,c满足a+b+c=0,向量a与b的夹角为60°,且|a|=|b|=1,则向量a与c的夹角为( ).
| A.30° | B.60° | C.120° | D.150° |
 的函数
的函数 图像的两个端点为
图像的两个端点为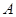 、
、 ,
, 是
是 .已知向量
.已知向量 ,若不等式
,若不等式 恒成立,则称函数
恒成立,则称函数 阶线性近似”.若函数
阶线性近似”.若函数 在
在 上“
上“