题目内容
某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第x个月的利润f(x)=
|
| 第x个月的利润 |
| 第x个月前的资金总和 |
| f(3) |
| 81+f(1)+f(2) |
(1)求g(10);
(2)求第x个月的当月利润率g(x);
(3)该企业经销此产品期间,哪个月的当月利润率最大,并求该月的当月利润率.
分析:(1)当1≤x≤20时,f(x)=1,易知f(1)=f(2)=f(3)=…=f(9)=f(10)=1,从而知g(10)=
=
(2)求第x个月的当月利润率,要考虑1≤x≤20,21≤x≤60时f(x)的值,代入g(x)=
即可.
(3)求那个月的当月利润率最大时,由(2)得出的分段函数,利用函数的单调性,基本不等式a+b≥2
(a>0,b>0,且a=b时取“=“)可得,解答如下:
| f(10) |
| 81+f(1)+f(2)+…+f(9) |
| 1 |
| 90 |
(2)求第x个月的当月利润率,要考虑1≤x≤20,21≤x≤60时f(x)的值,代入g(x)=
| 第x个月的利润 |
| 第x个月前的资金总和 |
(3)求那个月的当月利润率最大时,由(2)得出的分段函数,利用函数的单调性,基本不等式a+b≥2
| ab |
解答:解:(1)由题意得:f(1)=f(2)=f(3)=…═f(9)=f(10)=1
g(x)=
=
=
.
(2)当1≤x≤20时,f(1)=f(2)═f(x-1)=f(x)=1
∴g(x)=
=
=
=
.
当21≤x≤60时,
g(x)=
=
=
=
=
=
∴当第x个月的当月利润率
g(x)=
;
(3)当1≤x≤20时,g(x)=
是减函数,
此时g(x)的最大值为g(1)=
当21≤x≤60时,
g(x)=
=
≤
=
当且仅当x=
时,即x=40时,
g(x)max=
,又∵
>
,
∴当x=40时,g(x)max=
所以,该企业经销此产品期间,第40个月的当月利润率最大,最大值为
.
g(x)=
| f(10) |
| 81+f(1)+…+f(9) |
| 1 |
| 81+1+…+1 |
| 1 |
| 90 |
(2)当1≤x≤20时,f(1)=f(2)═f(x-1)=f(x)=1
∴g(x)=
| f(x) |
| 81+f(1)+…+f(x-1) |
| 1 |
| 81+1+…+1 |
| 1 |
| 81+(x-1) |
| 1 |
| x+80 |
当21≤x≤60时,
g(x)=
| f(x) |
| 81+f(1)+…+f(20)+f(21)+…+f(x-1) |
=
| ||
| 81+1+…+1+f(21)+…f(x-1) |
=
| ||||
81+20+
|
=
| ||||||
101+
|
=
| ||
101+
|
| 2x |
| x2-x+1600 |
∴当第x个月的当月利润率
g(x)=
|
(3)当1≤x≤20时,g(x)=
| 1 |
| x+80 |
此时g(x)的最大值为g(1)=
| 1 |
| 81 |
当21≤x≤60时,
g(x)=
| 2x |
| x2-x+1600 |
| 2 | ||
x+
|
| 2 | ||
2
|
| 2 |
| 79 |
当且仅当x=
| 1600 |
| x |
g(x)max=
| 2 |
| 79 |
| 2 |
| 79 |
| 1 |
| 81 |
∴当x=40时,g(x)max=
| 2 |
| 79 |
所以,该企业经销此产品期间,第40个月的当月利润率最大,最大值为
| 2 |
| 79 |
点评:本题是分段函数的应用题,借助分段函数考查反函数的单调性,基本不等式的应用,求分段函数的最值,综合性强,难度适中,值得学习.

练习册系列答案
相关题目
 个月的利润
个月的利润 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第 ,例如:
,例如: .
.  求
求 ; (Ⅱ)求第
; (Ⅱ)求第 ;
; 个月的利润
个月的利润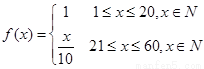 (单位:万元),
(单位:万元), 例如:
例如:
 ;
; ;
;
 个月的利润
个月的利润 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第 ,例如:
,例如: .
. 的表达式;
的表达式; 个月的利润
个月的利润 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第 ,例如:
,例如: .
.  ;
;  ;
;