题目内容
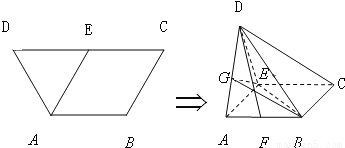
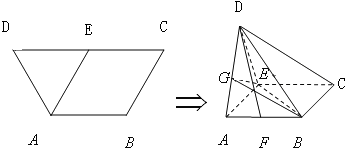
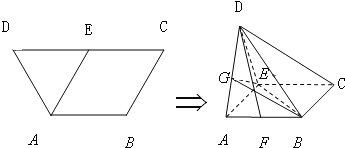
在如图1所示的等腰梯形ABCD中,AB∥CD,且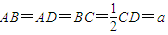 ,E为CD中点.若沿AE将三角形DAE折起,使平面DAE⊥平面ABCE,连接DB,DC,得到如图2所示的几何体D-ABCE,在图2中解答以下问题:
,E为CD中点.若沿AE将三角形DAE折起,使平面DAE⊥平面ABCE,连接DB,DC,得到如图2所示的几何体D-ABCE,在图2中解答以下问题:(Ⅰ)设F为AB中点,求证:DF⊥AC;
(Ⅱ)求二面角A-BD-C的正弦值.

【答案】分析:(Ⅰ)取AE中点H,连接HF,连接EB,利用面面垂直,证明线面垂直,即DH⊥平面ABCE,进一步证明AC⊥平面DHF,从而可得线线垂直;
(Ⅱ)建立空间直角坐标系,求出面DCB的法向量 ,面DAB的法向量
,面DAB的法向量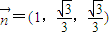 ,利用向量的夹角公式,可得二面角A-BD-C的正弦值.
,利用向量的夹角公式,可得二面角A-BD-C的正弦值.
解答: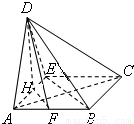 (Ⅰ)证明:取AE中点H,连接HF,连接EB
(Ⅰ)证明:取AE中点H,连接HF,连接EB
因为△DAE为等边三角形,所以DH⊥AE
因为平面DAE⊥平面ABCE,平面DAE∩平面ABCE=AE
所以DH⊥平面ABCE,
因为AC?平面ABCE
所以AC⊥DH…(2分)
因为ABCE为平行四边形,CE=BC=a
所以ABCE为菱形,所以AC⊥BE
因为H、F分别为AE、AB中点,所以HF∥BE
所以AC⊥HF…(4分)
因为HF?平面DHF,DH?平面DHF,且HF∩DH=H
所以AC⊥平面DHF,又DF?平面DHF
所以DF⊥AC…(6分)
(Ⅱ)解:连接BH,EB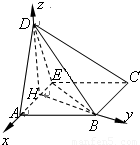
由题意得三角形ABE为等边三角形,所以BH⊥AE
由(Ⅰ)知DH⊥底面ABCE以H为原点,分别以HA,HB,HD所在直线为x,y,z轴
建立空间直角坐标系,如图所示
则
所以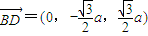 ,
,
设面DCB的法向量为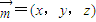 ,则
,则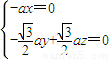
不妨设 …(8分)
…(8分)
设面DAB的法向量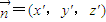 ,又
,又
则 ,取
,取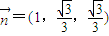 …(10分)
…(10分)
所以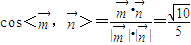
所以二面角A-BD-C的正弦值为 …(12分)
…(12分)
点评:本题看下线面垂直,考查线线垂直,考查面面角,考查利用空间向量解决空间角问题,属于中档题.
(Ⅱ)建立空间直角坐标系,求出面DCB的法向量
 ,面DAB的法向量
,面DAB的法向量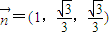 ,利用向量的夹角公式,可得二面角A-BD-C的正弦值.
,利用向量的夹角公式,可得二面角A-BD-C的正弦值.解答:
 (Ⅰ)证明:取AE中点H,连接HF,连接EB
(Ⅰ)证明:取AE中点H,连接HF,连接EB因为△DAE为等边三角形,所以DH⊥AE
因为平面DAE⊥平面ABCE,平面DAE∩平面ABCE=AE
所以DH⊥平面ABCE,
因为AC?平面ABCE
所以AC⊥DH…(2分)
因为ABCE为平行四边形,CE=BC=a
所以ABCE为菱形,所以AC⊥BE
因为H、F分别为AE、AB中点,所以HF∥BE
所以AC⊥HF…(4分)
因为HF?平面DHF,DH?平面DHF,且HF∩DH=H
所以AC⊥平面DHF,又DF?平面DHF
所以DF⊥AC…(6分)
(Ⅱ)解:连接BH,EB

由题意得三角形ABE为等边三角形,所以BH⊥AE
由(Ⅰ)知DH⊥底面ABCE以H为原点,分别以HA,HB,HD所在直线为x,y,z轴
建立空间直角坐标系,如图所示
则

所以
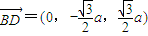 ,
,
设面DCB的法向量为
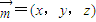 ,则
,则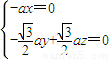
不妨设
 …(8分)
…(8分)设面DAB的法向量
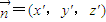 ,又
,又
则
 ,取
,取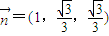 …(10分)
…(10分)所以
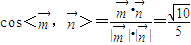
所以二面角A-BD-C的正弦值为
 …(12分)
…(12分)点评:本题看下线面垂直,考查线线垂直,考查面面角,考查利用空间向量解决空间角问题,属于中档题.

练习册系列答案
相关题目
 在如图1所示的等腰梯形ABCD中,AB∥CD,且
在如图1所示的等腰梯形ABCD中,AB∥CD,且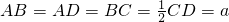 ,E为CD中点.若沿AE将三角形DAE折起,并连接DB,DC,得到如图2所示的几何体D-ABCE,在图2中解答以下问题:
,E为CD中点.若沿AE将三角形DAE折起,并连接DB,DC,得到如图2所示的几何体D-ABCE,在图2中解答以下问题: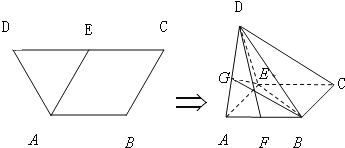
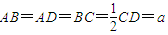 ,E为CD中点.若沿AE将三角形DAE折起,并连接DB,DC,得到如图2所示的几何体D-ABCE,在图2中解答以下问题:
,E为CD中点.若沿AE将三角形DAE折起,并连接DB,DC,得到如图2所示的几何体D-ABCE,在图2中解答以下问题: