题目内容
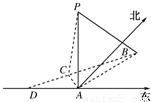 如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.
如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D、处,问此时船距岛A有多远?
【答案】分析:(1)先Rt△PAB、Rt△PAC中确定AB、AC的长,进而求得,∠CAB=30°+60°=90°,最后利用勾股定理求得BC,用里程除以时间即为船的速度.
(2)利用sin∠DCA=sin(180°-∠ACB)=sin∠ACB求得sin∠DCA的值,利用sin∠CDA=sin(∠ACB-30°)=sin∠ACB•cos30°-cos∠ACB•sin30°求得sin∠CDA的值,进而利用正弦定理求得AD.
解答:解:(1)在Rt△PAB中,∠APB=60°,PA=1,∴AB=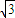 .
.
在Rt△PAC中,∠APC=30°,
∴AC=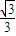 .
.
在△ACB中,∠CAB=30°+60°=90°,
∴BC=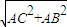 =
=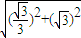 =
=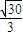 .
.
则船的航行速度为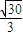 ÷
÷ =2
=2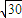 (千米/时).
(千米/时).
(2)在△ACD、中,∠DAC=90°-60°=30°,
sin∠DCA=sin(180°-∠ACB)=sin∠ACB=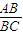 =
=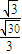 =
=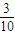
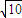 ,
,
sin∠CDA=sin(∠ACB-30°)
=sin∠ACB•cos30°-cos∠ACB•sin30°
=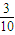
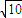 •
•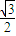 -
-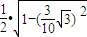
=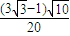 .
.
由正弦定理得 =
=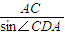 .
.
∴AD=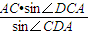 =
=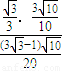 =
=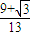 .
.
故此时船距岛A有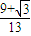 千米.
千米.
点评:本题组要考查正弦定理和余弦定理的灵活运用.考查考生运用数学知识解决实际问题的能力.
(2)利用sin∠DCA=sin(180°-∠ACB)=sin∠ACB求得sin∠DCA的值,利用sin∠CDA=sin(∠ACB-30°)=sin∠ACB•cos30°-cos∠ACB•sin30°求得sin∠CDA的值,进而利用正弦定理求得AD.
解答:解:(1)在Rt△PAB中,∠APB=60°,PA=1,∴AB=
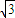 .
.在Rt△PAC中,∠APC=30°,
∴AC=
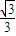 .
.在△ACB中,∠CAB=30°+60°=90°,
∴BC=
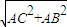 =
=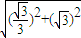 =
=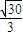 .
.则船的航行速度为
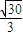 ÷
÷ =2
=2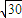 (千米/时).
(千米/时).(2)在△ACD、中,∠DAC=90°-60°=30°,
sin∠DCA=sin(180°-∠ACB)=sin∠ACB=
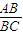 =
=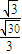 =
=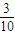
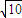 ,
,sin∠CDA=sin(∠ACB-30°)
=sin∠ACB•cos30°-cos∠ACB•sin30°
=
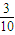
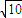 •
•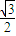 -
-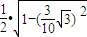
=
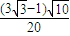 .
.由正弦定理得
 =
=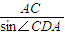 .
.∴AD=
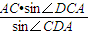 =
=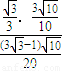 =
=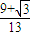 .
.故此时船距岛A有
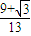 千米.
千米.点评:本题组要考查正弦定理和余弦定理的灵活运用.考查考生运用数学知识解决实际问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
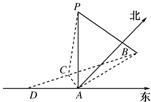 如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.
如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.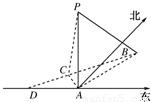 如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.
如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.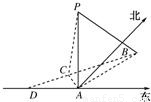 如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.
如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.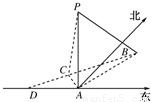 如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.
如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.