题目内容
已知命题P:方程a2x2+ax-2=0在[-1,1]上有解,命题Q:不等式x+|x-2a|>1的解集为R,如果P,Q中有且仅有一个正确,求a的取值范围.分析:首先解出两个命题成立时对应的a的范围,再依据P,Q中有且仅有一个正确正确的条件,解出符合条件的a的范围.
解答:解:对于命题P:a2x2+ax-2=0可变为(ax+2)×(ax-1)=0,当a=0时方程无意义,故a不为0,由此可解得方程的根为x=-
或x=
当-
∈[-1,1]时,必有
∈[-1,1],故只需
∈[-1,1]成立即可,解得a≥1或a≤-1
对于命题Q:不等式x+|x-2a|>1可以变为|x-2a|>1-x,考察不等式两边表达式对应的函数图象,如图只需2a>1,即a>

∵P,Q中有且仅有一个正确
若P真Q假则可得a≤-1
若P假Q真,则可得
<a<1
综上,当a≤-1或
<a<1时P,Q中有且仅有一个正确
答:a≤-1或
<a<1
| 2 |
| a |
| 1 |
| a |
当-
| 2 |
| a |
| 1 |
| a |
| 1 |
| a |
对于命题Q:不等式x+|x-2a|>1可以变为|x-2a|>1-x,考察不等式两边表达式对应的函数图象,如图只需2a>1,即a>
| 1 |
| 2 |

∵P,Q中有且仅有一个正确
若P真Q假则可得a≤-1
若P假Q真,则可得
| 1 |
| 2 |
综上,当a≤-1或
| 1 |
| 2 |
答:a≤-1或
| 1 |
| 2 |
点评:本题考点是命题真假性的判断,此类题考试方式经常与不等式或者方程有解等知识一起出现,其特征是大的判断是命题的真假性与命题的关系,细节上是解方程等.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
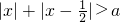 恒成立;若P或q为真,P且q为假,求实数a的取值范围.
恒成立;若P或q为真,P且q为假,求实数a的取值范围. 恒成立;若P或q为真,P且q为假,求实数a的取值范围.
恒成立;若P或q为真,P且q为假,求实数a的取值范围.