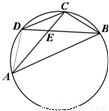
题目内容
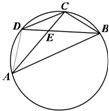 如图,在圆内接四边形ABCD中,对角线AC,BD相交于点E.已知BC=CD=2
如图,在圆内接四边形ABCD中,对角线AC,BD相交于点E.已知BC=CD=2| 3 |
分析:根据相同的弦对应相同的弧和同弧所对的圆周角相等,得到∠CAB=30°,根据两个三角形有两对角对应相等,得到两个三角形相似,根据对应边成比例得到BE=2EC,利用余弦定理做出CE的长度,得到结果.
解答:解:∵∠ACD=∠ABE,∠CDB=∠CAB,
∴△CDE∽△ABE,
∵AE=2EC,
∴BE=2ED,BE=
BD=
=4
∵∠CBD=30°,BC=CD
∴∠CAB=30°,∠CDB=30°,
在△DEC中,CE2=16+12-2×4×2
×
=4,
∴CE=2,
∴AC=6,
故答案为:30°;6.
∴△CDE∽△ABE,
∵AE=2EC,
∴BE=2ED,BE=
| 2 |
| 3 |
| 2 |
| 3 |
12+12-2×2
|
∵∠CBD=30°,BC=CD
∴∠CAB=30°,∠CDB=30°,

在△DEC中,CE2=16+12-2×4×2
| 3 |
| ||
| 2 |
∴CE=2,
∴AC=6,
故答案为:30°;6.
点评:本题是一个比较简单的综合题目,在解题时,注意同弧所对的圆周角相等的重复使用,还有一个用的不是很多的结论即在同一个圆中,等弦对等弧

练习册系列答案
相关题目
 中,对角线
中,对角线 ,
,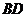 相交于点
相交于点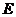 。已知
。已知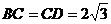 ,
,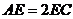 ,
,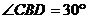 ,则
,则 _____________,
_____________,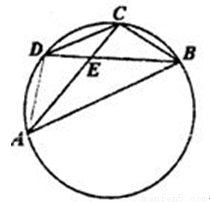
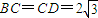 ,AE=2EC,∠CBD=30°,则∠CAB= ,AC的长是 .
,AE=2EC,∠CBD=30°,则∠CAB= ,AC的长是 .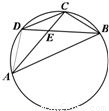
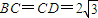 ,AE=2EC,∠CBD=30°,则∠CAB= ,AC的长是 .
,AE=2EC,∠CBD=30°,则∠CAB= ,AC的长是 .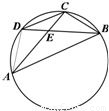
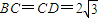 ,AE=2EC,∠CBD=30°,则∠CAB= ,AC的长是 .
,AE=2EC,∠CBD=30°,则∠CAB= ,AC的长是 .