题目内容
已知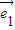 、
、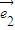 是两个不共线的平面向量,向量
是两个不共线的平面向量,向量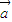 =2
=2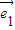 -
-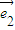 ,
,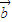 =
=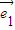 +λ
+λ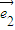 (λ∈R),若
(λ∈R),若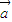 ∥
∥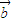 ,则λ= .
,则λ= .
【答案】分析:通过2个向量共线的条件得到2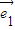 -
-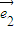 =k(
=k(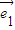 +λ
+λ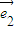 ),又
),又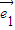 、
、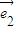 不共线,得到
不共线,得到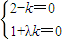 ,解此方程组即可求得λ的值.
,解此方程组即可求得λ的值.
解答:解:∵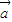 与
与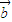 共线,∴
共线,∴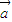 =k
=k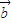 (k∈R),
(k∈R),
即2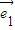 -
-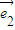 =k(
=k(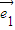 +λ
+λ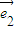 ),
),
∴(2-k)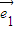 -(1+λk)
-(1+λk)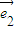 =0
=0
∵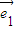 、
、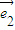 不共线,∴
不共线,∴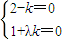 ,
,
解得λ=- ,
,
故答案为:- .
.
点评:本题考查2个向量共线的条件、共面向量基本定理的应用.属基础题.
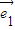 -
-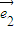 =k(
=k(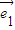 +λ
+λ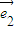 ),又
),又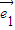 、
、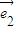 不共线,得到
不共线,得到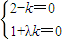 ,解此方程组即可求得λ的值.
,解此方程组即可求得λ的值.解答:解:∵
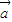 与
与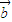 共线,∴
共线,∴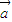 =k
=k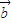 (k∈R),
(k∈R),即2
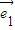 -
-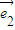 =k(
=k(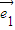 +λ
+λ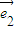 ),
),∴(2-k)
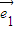 -(1+λk)
-(1+λk)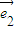 =0
=0∵
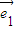 、
、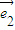 不共线,∴
不共线,∴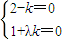 ,
,解得λ=-
 ,
,故答案为:-
 .
.点评:本题考查2个向量共线的条件、共面向量基本定理的应用.属基础题.

练习册系列答案
相关题目
 已知
已知 、
、 是两个不共线的向量,O是同一平面内的一个定点,
是两个不共线的向量,O是同一平面内的一个定点, ,则以下结论中,错误的是
,则以下结论中,错误的是 .
.
 .
D.以上选项A、B、C不全对
.
D.以上选项A、B、C不全对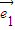 ,
,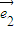 是两个不共线的单位向量,向量
是两个不共线的单位向量,向量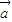 =3
=3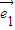 -
-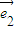 ,
, =t
=t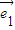 +2
+2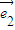 ,且
,且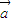 ∥
∥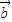 ,则t=( )
,则t=( )