题目内容
(理)(1)求证:mC
=nC
,(m,n∈N*,n≥m≥2);
(2)现共有4男生,3女生排成一排,
①女生不站在两端,共有多少种排法;
②男生都排在一起,共有多少种排法;
③女生互不相邻,共有多少种排法;
④男生A,B不相邻,男生C,D要相邻,共有多少种排法.
m n |
m-1 n-1 |
(2)现共有4男生,3女生排成一排,
①女生不站在两端,共有多少种排法;
②男生都排在一起,共有多少种排法;
③女生互不相邻,共有多少种排法;
④男生A,B不相邻,男生C,D要相邻,共有多少种排法.
分析:(1)利用组合数的计算公式即可证明;
(2))①特殊位置优先考虑:先选2名男生排在两头并且可以交换位置有
种方法,剩下的2名男生与3名女生全排列可有
种方法,由分步乘法原理即可求出;
②相邻用捆绑法:男生都排在一起可以交换位置有
种方法,与3名女生全排列有
种方法,由分步乘法原理即可求出;
③不相邻用插空法:先把4名男生排好但是可以交换位置有
种方法,而4名男生之间的3个空隙加上两边共有5个空隙,选出3个插入3名女生可有
种方法,由分步乘法原理即可得出;
④相邻用捆绑法、不相邻用插空法:把2名C,D男生捆绑成一个元素但是可以交换位置与3名女生全排列有
种方法,把2名男生A,B插入上述4个元素之间及其两边共5个空隙中可有
种方法,由分步乘法原理即可得出.
(2))①特殊位置优先考虑:先选2名男生排在两头并且可以交换位置有
| A | 2 4 |
| A | 5 5 |
②相邻用捆绑法:男生都排在一起可以交换位置有
| A | 4 4 |
| A | 4 4 |
③不相邻用插空法:先把4名男生排好但是可以交换位置有
| A | 4 4 |
| A | 3 5 |
④相邻用捆绑法、不相邻用插空法:把2名C,D男生捆绑成一个元素但是可以交换位置与3名女生全排列有
| A | 2 2 |
| A | 4 4 |
| A | 2 5 |
解答:(1)证明:左边=
=
,右边=
=
.
∴左边=右边.
(2)解:①先选2名男生排在两头并且可以交换位置有
种方法,剩下的2名男生与3名女生全排列可有
种方法,由分步乘法原理共有
=1440种方法;
②男生都排在一起可以交换位置有
种方法,与3名女生全排列有
种方法,由分步乘法原理共有
=576种方法;
③先把4名男生排好但是可以交换位置有
种方法,而4名男生之间的3个空隙加上两边共有5个空隙,选出3个插入3名女生可有
种方法,由分步乘法原理共有
=1440种方法;
④把2名C,D男生捆绑成一个元素但是可以交换位置与3名女生全排列有
种方法,把2名男生A,B插入上述4个元素之间及其两边共5个空隙中可有
种方法,由分步乘法原理共有
=960种方法.
m
| ||
| m! |
| ||
| (m-1)! |
n
| ||
| (m-1)! |
| ||
| (m-1)! |
∴左边=右边.
(2)解:①先选2名男生排在两头并且可以交换位置有
| A | 2 4 |
| A | 5 5 |
| A | 2 4 |
| A | 5 5 |
②男生都排在一起可以交换位置有
| A | 4 4 |
| A | 4 4 |
| A | 4 4 |
| A | 4 4 |
③先把4名男生排好但是可以交换位置有
| A | 4 4 |
| A | 3 5 |
| A | 4 4 |
| A | 3 5 |
④把2名C,D男生捆绑成一个元素但是可以交换位置与3名女生全排列有
| A | 2 2 |
| A | 4 4 |
| A | 2 5 |
| A | 2 2 |
| A | 4 4 |
| A | 2 5 |
点评:熟练掌握排列与组合数的计算公式、特殊位置优先考虑、相邻用捆绑法、不相邻用插空法等是解题的关键.

练习册系列答案
相关题目
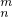 =nC
=nC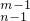 ,(m,n∈N*,n≥m≥2);
,(m,n∈N*,n≥m≥2); =nC
=nC ,(m,n∈N*,n≥m≥2);
,(m,n∈N*,n≥m≥2);