题目内容
 由计算机随机选出大批正整数,取其最高位数字(如 35为3,110为1)的次数构成一个分布,已知这个分布中,数字1,2,3,…,9出现的概率正好构成一个首项为
由计算机随机选出大批正整数,取其最高位数字(如 35为3,110为1)的次数构成一个分布,已知这个分布中,数字1,2,3,…,9出现的概率正好构成一个首项为| 1 | 5 |
(1)求x的概率分布;
(2)求x的期望Ex.
分析:(1)设出数列的公差,根据数字1,2,3,…,9出现的概率正好构成一个首项为
的等差数列,和分布列中所有的概率之和是1,得到数列的方差,得到各个变量对应的概率,写出分布列.
(2)根据上一问的分布列求出变量的期望值.
| 1 |
| 5 |
(2)根据上一问的分布列求出变量的期望值.
解答:解:(1)根据题意设P(ξ=n)=an(n═1,2,…,9),
公差为d,
∵数字1,2,3,…,9出现的概率正好构成一个首项为
的等差数列
∴
×9+
×9×8d=1,
∴d=-
,
∴P(ξ=n)=
-(n-1)
(n═1,2,…,9)
∴分布如下:
(2)根据第一问的分布列写出期望
Ex=
=
公差为d,
∵数字1,2,3,…,9出现的概率正好构成一个首项为
| 1 |
| 5 |
∴
| 1 |
| 5 |
| 1 |
| 2 |
∴d=-
| 1 |
| 45 |
∴P(ξ=n)=
| 1 |
| 5 |
| 1 |
| 45 |
∴分布如下:
| ξ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||||||||||
| P |
|
|
|
|
|
|
|
|
|
Ex=
| 2×(1×9+2×8+3×7+4×6)+25 |
| 45 |
| 11 |
| 3 |
点评:本题考查离散型随机变量的分布列和期望值,考查等差数列的通项,在解题时注意分布列的性质的应用,正确利用方程思想解决概率问题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 由计算机随机选出大批正整数,取其最高位数字(如 35为3,110为1)的次数构成一个分布,已知这个分布中,数字1,2,3,…,9出现的概率正好构成一个首项为
由计算机随机选出大批正整数,取其最高位数字(如 35为3,110为1)的次数构成一个分布,已知这个分布中,数字1,2,3,…,9出现的概率正好构成一个首项为 的等差数列.现从这批正整数中任取一个,记其最高位数字为x (x=1,2,…,9).
的等差数列.现从这批正整数中任取一个,记其最高位数字为x (x=1,2,…,9).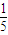 的等差数列.现从这批正整数中任取一个,记其最高位数字为x (x=1,2,…,9).
的等差数列.现从这批正整数中任取一个,记其最高位数字为x (x=1,2,…,9).