Question

点P在直线l：y=x-1上，若存在过P的直线交抛物线y=x²于A，B两点，且|PA|=|AB|，则称点P为“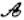点”，那么下列结论中正确的是

1. A.
   直线l上的所有点都是“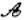点”
2. B.
   直线l上仅有有限个点是“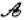点”
3. C.
   直线l上的所有点都不是“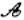点”
4. D.
   直线l上有无穷多个点（点不是所有的点）是“点”

Answer 1

A
分析：根据题设方程分别设出A，P的坐标，进而B的坐标可表示出，把A，B的坐标代入抛物线方程联立消去y，求得判别式大于0恒成立，可推断出方程有解，进而可推断出直线l上的所有点都符合．
解答：设A（m，n），P（x，x-1）则，B（2m-x，2n-x+1）
∵A，B在y=x²上
∴n=m²，2n-x+1=（2m-x）²
消去n，整理得关于x的方程
x²-（4m-1 ）x+2m²-1=0
∵△=8m²-8m+5＞0恒成立，
∴方程恒有实数解，
∴故选A．
点评：本题主要考查了直线与圆锥曲线的位置关系．一般是把直线与圆锥曲线方程联立，解决直线与圆锥曲线的交点个数时，利用判别式来判断．