题目内容
若函数f（x）=ax3-bx+4，当x=2时，函数f（x）有极值为-| 4 | 3 |
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若f（x）=k有3个解，求实数k的取值范围．
分析：（1）先对函数进行求导，然后根据f（2）=-
．f'（2）=0可求出a，b的值，进而确定函数的解析式．
（2）根据（1）中解析式然后求导，然后令导函数等于0求出x的值，然后根据函数的单调性与其导函数的正负之间的关系确定单调性，进而确定函数的大致图象，最后找出k的范围．
| 4 |
| 3 |
（2）根据（1）中解析式然后求导，然后令导函数等于0求出x的值，然后根据函数的单调性与其导函数的正负之间的关系确定单调性，进而确定函数的大致图象，最后找出k的范围．
解答：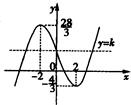
解：（Ⅰ）f′（x）=3ax2-b
由题意；
，解得
，
∴所求的解析式为f(x)=
x3-4x+4
（Ⅱ）由（1）可得f′（x）=x2-4=（x-2）（x+2）
令f′（x）=0，得x=2或x=-2，
∴当x＜-2时，f′（x）＞0，当-2＜x＜2时，f′（x）＜0，当x＞2时，f′（x）＞0
因此，当x=-2时，f（x）有极大值
，
当x=2时，f（x）有极小值-
，
∴函数f(x)=
x3-4x+4的图象大致如图．
由图可知：-
＜k＜
．
解：（Ⅰ）f′（x）=3ax2-b由题意；
|
|
∴所求的解析式为f(x)=
| 1 |
| 3 |
（Ⅱ）由（1）可得f′（x）=x2-4=（x-2）（x+2）
令f′（x）=0，得x=2或x=-2，
∴当x＜-2时，f′（x）＞0，当-2＜x＜2时，f′（x）＜0，当x＞2时，f′（x）＞0
因此，当x=-2时，f（x）有极大值
| 28 |
| 3 |
当x=2时，f（x）有极小值-
| 4 |
| 3 |
∴函数f(x)=
| 1 |
| 3 |
由图可知：-
| 4 |
| 3 |
| 28 |
| 3 |
点评：本题主要考查函数的单调性、极值与其导函数之间的关系．导数是高等数学下放到高中的内容，是高考的热点问题，每年必考，要给予充分重视．
练习册系列答案
相关题目