题目内容
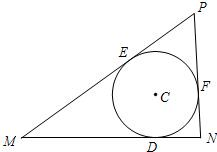 已知点D在定线段MN上,且|MN|=3,|DN|=1,一个动圆C过点D且与MN相切,分别过M、N作圆C的另两条切线交于点P.
已知点D在定线段MN上,且|MN|=3,|DN|=1,一个动圆C过点D且与MN相切,分别过M、N作圆C的另两条切线交于点P.(Ⅰ)建立适当的直角坐标系,求点P的轨迹方程;
(Ⅱ)过点M作直线l与所求轨迹交于两个不同的点A、B,若(
| MA |
| MB |
| MA |
| MB |
| 3 |
| 3 |
分析:(Ⅰ)以直线MN为x轴,MN的中点为坐标原点O,建立直角坐标系xOy.由题意知点P的轨迹是以M、N为焦点,实轴长为2的双曲线(不包含顶点),其轨迹方程为x2-
=1(y≠0).
(Ⅱ)由题设条件知
=±λ
,设A(x1,y1),B(x2,y2),则
=(x1+2,y1),
=(x2+2,y2)设AB:my=x+2,代入x2-
=1得,(3m2-1)y2-12my+9=0.所以
.由此入手能够求出直线l与直线MN夹角θ的取值范围.
| y2 |
| 3 |
(Ⅱ)由题设条件知
| MA |
| MB |
| MA |
| MB |
| y2 |
| 3 |
|
解答:解:(Ⅰ)以直线MN为x轴,MN的中点为坐标原点O,
建立直角坐标系xOy. (1分)
∵PM-PN=(PE+EM)-(PF+FN)=MD-ND=2
或PM-PN=(PE+EM)-(PF+FN)=MD-ND=-2 (3分)
∴点P的轨迹是以M、N为焦点,实轴长为2的双曲线(不包含顶点),
其轨迹方程为x2-
=1(y≠0) (5分)
(Ⅱ)∵(
+λ
)•(
-λ
)=0,且λ∈[2-
,2+
],
∴
=±λ
,(6分)
设A(x1,y1),B(x2,y2),则
=(x1+2,y1),
=(x2+2,y2)
设AB:my=x+2,代入x2-
=1得,3(my-2)2-y2-3=0,
即(3m2-1)y2-12my+9=0.
∴
(7分)
①当
=λ
时,y1=λy2,∴
(8分)
得,
=
,(9分)
∴
=2+λ+
∈[4,6],即4≤
≤6.
∴
解得,m2≥3,故tan2θ≤
(10分)
②当
=-λ
时y1=-λy2,∴
(11分)
得,
=
,即2-(λ+
)=
.
∵λ∈[2-
,2+
],λ+
∈[2,4]
∴2-(λ+
)∈[-2,0],即-2≤
≤0.
∴
即m2≤
,故tan2θ≥11. (13分)
由①、②得tan2θ≤
或tan2θ≥11.
则夹角θ∈(0,
]∪arctan
,
),(14分)
∵tanθ不存在时,直线l符合条件,故θ=
时,符合题意.
∴θ∈(0,
]∪[arctan
,
). (15分)
建立直角坐标系xOy. (1分)
∵PM-PN=(PE+EM)-(PF+FN)=MD-ND=2
或PM-PN=(PE+EM)-(PF+FN)=MD-ND=-2 (3分)
∴点P的轨迹是以M、N为焦点,实轴长为2的双曲线(不包含顶点),
其轨迹方程为x2-
| y2 |
| 3 |
(Ⅱ)∵(
| MA |
| MB |
| MA |
| MB |
| 3 |
| 3 |
∴
| MA |
| MB |
设A(x1,y1),B(x2,y2),则
| MA |
| MB |
设AB:my=x+2,代入x2-
| y2 |
| 3 |
即(3m2-1)y2-12my+9=0.
∴
|
①当
| MA |
| MB |
|
| (1)2 |
| (2)2 |
| (1+λ)2 |
| λ |
| 16m2 |
| 3m2-1 |
∴
| 16m2 |
| 3m2-1 |
| 1 |
| λ |
| 16m2 |
| 3m2-1 |
∴
|
| 1 |
| 3 |
②当
| MA |
| MB |
|
| (3)2 |
| (4)2 |
| (1-λ)2 |
| -λ |
| 16m2 |
| 3m2-1 |
| 1 |
| λ |
| 16m2 |
| 3m2-1 |
∵λ∈[2-
| 3 |
| 3 |
| 1 |
| λ |
∴2-(λ+
| 1 |
| λ |
| 16m2 |
| 3m2-1 |
∴
|
| 1 |
| 11 |
由①、②得tan2θ≤
| 1 |
| 3 |
则夹角θ∈(0,
| π |
| 6 |
| 11 |
| π |
| 2 |
∵tanθ不存在时,直线l符合条件,故θ=
| π |
| 2 |
∴θ∈(0,
| π |
| 6 |
| 11 |
| π |
| 2 |
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细解答.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
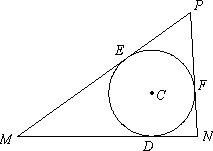
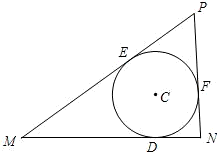 已知点D在定线段MN上,且|MN|=3,|DN|=1,一个动圆C过点D且与MN相切,分别过M、N作圆C的另两条切线交于点P.
已知点D在定线段MN上,且|MN|=3,|DN|=1,一个动圆C过点D且与MN相切,分别过M、N作圆C的另两条切线交于点P. +λ
+λ )•(
)•( ,2+
,2+ +λ
+λ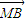 )•(
)•(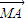 -λ
-λ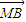 )=0,且λ∈[2-
)=0,且λ∈[2-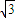 ,2+
,2+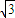 ],求直线l与直线MN夹角θ的取值范围.
],求直线l与直线MN夹角θ的取值范围.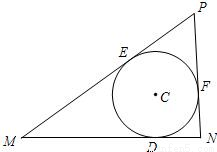
 +λ
+λ )•(
)•( -λ
-λ )=0,且λ∈[2-
)=0,且λ∈[2- ,2+
,2+ ],求直线l与直线MN夹角θ的取值范围.
],求直线l与直线MN夹角θ的取值范围.