题目内容
设S是由满足下列两个条件的实数组成的集合:
①不含1;
②a∈S,则
∈S.
问:
(Ⅰ)如果2∈S,研究S中元素个数,并求出这些元素;
(Ⅱ)集合S中元素的个数能否只有一个?
①不含1;
②a∈S,则
| 1 | 1-a |
问:
(Ⅰ)如果2∈S,研究S中元素个数,并求出这些元素;
(Ⅱ)集合S中元素的个数能否只有一个?
分析:(Ⅰ)如果2∈S,根据条件进行递推即可确定其他元素;
(Ⅱ)利用集合S中元素的个数能只有一个,得到方程
=a只有一解即可,考查方程解的情况.
(Ⅱ)利用集合S中元素的个数能只有一个,得到方程
| 1 |
| 1-a |
解答:解:(Ⅰ)如果2∈S,根据条件得
=-1∈S,
=
∈S,
=2∈S,
=-1∈S,此时元素进行循环,所以集合中还有元素-1,
.
所以集合中的元素为-1,2,
.
(Ⅱ)若集合S中元素的个数只有一个,则方程
=a有解,得a2-a+1=0,但该方程无解.
故集合S中元素的个数不可能只有一个元素.
| 1 |
| 1-2 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
| 1 | ||
1-
|
| 1 |
| 1-2 |
| 1 |
| 2 |
所以集合中的元素为-1,2,
| 1 |
| 2 |
(Ⅱ)若集合S中元素的个数只有一个,则方程
| 1 |
| 1-a |
故集合S中元素的个数不可能只有一个元素.
点评:本题主要考查集合元素的判断和推导,考查学生的分析能力.

练习册系列答案
相关题目
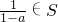 .
.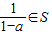 .
.