题目内容
如图,AD⊥平面ABC,AD∥CE,AC=AD=AB=1,∠BAC=90°,凸多面体ABCED的体积为 ,F为BC的中点.
,F为BC的中点.(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:平面BDE⊥平面BCE.

【答案】分析:(Ⅰ)先求CE的长,再取BE的中点G,连结GF,GD,证明四边形ADGF为平行四边形,可得AF∥DG,利用线面平行的判定,即可证明AF∥平面BDE;
(Ⅱ)先证明AF⊥面BCE,根据DG∥AF,可得DG⊥面BCE,利用面面垂直的判定,即可证明平面BDE⊥平面BCE.
解答:证明: (Ⅰ)∵AD⊥平面ABC,AC?面ABC,AB?面ABC,
(Ⅰ)∵AD⊥平面ABC,AC?面ABC,AB?面ABC,
∴AD⊥AC,AD⊥AB,
∵AD∥CE,∴CE⊥AC
∴四边形ACED为直角梯形.…(1分)
又∵∠BAC=90°,∴AB⊥AC,∴AB⊥面ACED.…(2分)
∴凸多面体ABCED的体积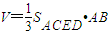 =
=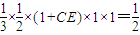
∴CE=2.…(3分)
取BE的中点G,连结GF,GD,则GF∥EC,GF= CE=1,
CE=1,
∴GF∥AD,GF=AD,四边形ADGF为平行四边形,
∴AF∥DG.…(5分)
又∵GD?面BDE,AF?面BDE,
∴AF∥平面BDE.…(7分)
(Ⅱ)∵AB=AC,F为BC的中点,∴AF⊥BC.…(8分)
由(Ⅰ)知AD⊥平面ABC,AD∥GF,∴GF⊥面ABC.
∵AF?面ABC,∴AF⊥GF.…(9分)
又BC∩GF=F,∴AF⊥面BCE.…(10分)
又∵DG∥AF,∴DG⊥面BCE.…(11分)
∵DG?面BDE,∴面BDE⊥面BCE.…(12分)
点评:本题考查线面平行、面面垂直,考查几何体体积的计算,正确运用线面平行、面面垂直的判定方法是关键.
(Ⅱ)先证明AF⊥面BCE,根据DG∥AF,可得DG⊥面BCE,利用面面垂直的判定,即可证明平面BDE⊥平面BCE.
解答:证明:
 (Ⅰ)∵AD⊥平面ABC,AC?面ABC,AB?面ABC,
(Ⅰ)∵AD⊥平面ABC,AC?面ABC,AB?面ABC,∴AD⊥AC,AD⊥AB,
∵AD∥CE,∴CE⊥AC
∴四边形ACED为直角梯形.…(1分)
又∵∠BAC=90°,∴AB⊥AC,∴AB⊥面ACED.…(2分)
∴凸多面体ABCED的体积
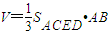 =
=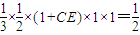
∴CE=2.…(3分)
取BE的中点G,连结GF,GD,则GF∥EC,GF=
 CE=1,
CE=1,∴GF∥AD,GF=AD,四边形ADGF为平行四边形,
∴AF∥DG.…(5分)
又∵GD?面BDE,AF?面BDE,
∴AF∥平面BDE.…(7分)
(Ⅱ)∵AB=AC,F为BC的中点,∴AF⊥BC.…(8分)
由(Ⅰ)知AD⊥平面ABC,AD∥GF,∴GF⊥面ABC.
∵AF?面ABC,∴AF⊥GF.…(9分)
又BC∩GF=F,∴AF⊥面BCE.…(10分)
又∵DG∥AF,∴DG⊥面BCE.…(11分)
∵DG?面BDE,∴面BDE⊥面BCE.…(12分)
点评:本题考查线面平行、面面垂直,考查几何体体积的计算,正确运用线面平行、面面垂直的判定方法是关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
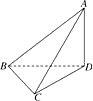 如图,AD⊥平面BCD,∠BCD=90°,AD=BC=CD=a,则二面角C-AB-D的大小为
如图,AD⊥平面BCD,∠BCD=90°,AD=BC=CD=a,则二面角C-AB-D的大小为
 (2013•临沂二模)如图,AD⊥平面ABC,AD∥CE,AC=AD=AB=1,∠BAC=90°,凸多面体ABCED的体积为
(2013•临沂二模)如图,AD⊥平面ABC,AD∥CE,AC=AD=AB=1,∠BAC=90°,凸多面体ABCED的体积为 所在平面与正
所在平面与正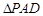 所在平面互相垂直,
所在平面互相垂直,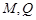 分别为
分别为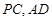 的中点.
的中点.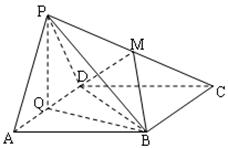
 -
- 的体积;
的体积;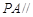 平面
平面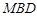 ;
;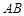 上是否存在一点
上是否存在一点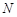 ,使得平面
,使得平面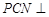 平面
平面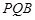 ?若存在,试指出点
?若存在,试指出点 如图,AD⊥平面BCD,∠BCD=90°,AD=BC=CD=a,则二面角C-AB-D的大小为 .
如图,AD⊥平面BCD,∠BCD=90°,AD=BC=CD=a,则二面角C-AB-D的大小为 .