题目内容
在平行四边形ABCD中, ,则锐角A的最大值为( )
,则锐角A的最大值为( )
A.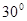 | B.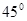 | C. | D.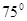 |
C
解析试题分析:因为 中,
中, ,
, ,
,
因为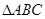 中,
中,  ,
, ,
,
因为 ,所以
,所以 ,
,
所以 ,又因为
,又因为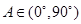 ,
,
所以 ,所以锐角A的最大值为
,所以锐角A的最大值为 .
.
考点: 余弦定理在解三角形当中的应用,基本不等式,余弦函数的值域.
点评:本小题利用 和
和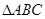 的
的 和
和 互补,然后在这两个三角形中分别利用余弦定理表示出AC,BD,再根据
互补,然后在这两个三角形中分别利用余弦定理表示出AC,BD,再根据 ,从而得到
,从而得到 ,再使用基本不等式求出cosA的取值范围,进而得到A的范围.
,再使用基本不等式求出cosA的取值范围,进而得到A的范围.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
下列函数中,最小正周期为 ,且图象关于直线
,且图象关于直线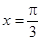 对称的是( ).
对称的是( ).
A. | B.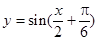 |
C. | D.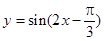 |
锐角△ABC中,若A=2B,则 的取值范围是( )
的取值范围是( )
| A.(1,2) | B.(1, ) ) | C.( ) ) | D.(  ) ) |
函数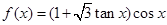 的最小正周期为( )
的最小正周期为( )
A.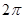 | B.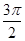 | C. | D. |
已知函数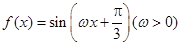 的最小正周期为
的最小正周期为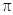 ,则函数
,则函数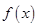 的图象( )
的图象( )
A.关于点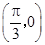 对称 对称 | B.关于直线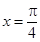 对称 对称 |
C.关于点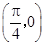 对称 对称 | D.关于直线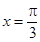 对称 对称 |
 中角
中角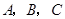 的对边分别为
的对边分别为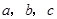 ,
,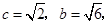 ,
,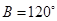 ,则
,则 为( )
为( )
A. | B.2 | C. | D.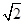 |
为了得到函数 的图象,只需把函数
的图象,只需把函数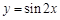 的图象
的图象
A.向左平移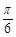 个长度单位 个长度单位 | B.向右平移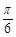 个长度单位 个长度单位 |
C.向右平移 个长度单位 个长度单位 | D.向左平移 个长度单位 个长度单位 |
设函数 ,则
,则
A.y= 在 在 单调递减,其图像关于直线 单调递减,其图像关于直线 对称 对称 |
B.y= 在 在 单调递增,其图像关于直线 单调递增,其图像关于直线 对称 对称 |
C.y= 在 在 单调递减,其图像关于直线 单调递减,其图像关于直线 对称 对称 |
D.y= 在 在 单调递增,其图像关于直线 单调递增,其图像关于直线 对称 对称 |
 的图像为C,如下结论中正确的是( )
的图像为C,如下结论中正确的是( )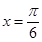 对称
对称  对称
对称 在区间
在区间 内是增函数
内是增函数 的图像向右平移
的图像向右平移 个单位长度可以得到图像C。
个单位长度可以得到图像C。