题目内容
向量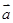 与
与 夹角为
夹角为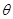 ,且
,且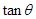 =
=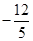 ,则
,则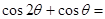
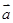 与
与 夹角为
夹角为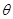 ,且
,且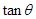 =
=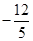 ,则
,则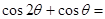
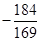
试题分析:根据题意,由于向量
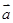 与
与 夹角为
夹角为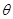 ,且
,且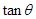 =
=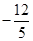 ,根据同角关系式可得
,根据同角关系式可得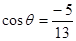 那么可知夹角为钝角,所以
那么可知夹角为钝角,所以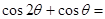
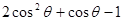 =
=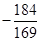 ,故可知结论为
,故可知结论为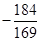 。
。点评:主要是考查了向量的数量积以及二倍角公式的运用,属于基础题。

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
题目内容
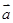 与
与 夹角为
夹角为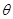 ,且
,且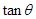 =
=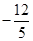 ,则
,则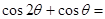
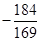
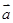 与
与 夹角为
夹角为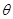 ,且
,且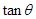 =
=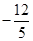 ,根据同角关系式可得
,根据同角关系式可得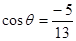 那么可知夹角为钝角,所以
那么可知夹角为钝角,所以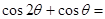
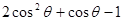 =
=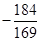 ,故可知结论为
,故可知结论为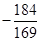 。
。
 同步练习强化拓展系列答案
同步练习强化拓展系列答案