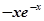题目内容
给出定义:若函数 在D上可导,即
在D上可导,即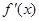 存在,且导函数
存在,且导函数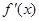 在D上也可导,则称
在D上也可导,则称 在D上存在二阶导函数,记
在D上存在二阶导函数,记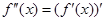 ,若
,若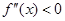 在D上恒成立,则称
在D上恒成立,则称 在D上为凸函数,以下四个函数在(0,
在D上为凸函数,以下四个函数在(0,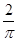 )上不是凸函数的是( )
)上不是凸函数的是( )
A.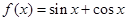 B.
B. C.
C.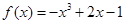 D.
D.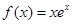
【答案】
D
【解析】解:对于f(x)=sinx+cosx,f′(x)=cosx-sinx,f″(x)=-sinx-cosx,当x∈(0,π 2 )时,f″(x)<0,故为凸函数,排除A;
对于f(x)=lnx-2x,f′(x)=1 /x -2,f″(x)=-1 /x 2 ,当x∈(0,π /2 )时,f″(x)<0,故为凸函数,排除B;
对于f(x)=-x3+2x-1,f′(x)=-3x2+2,f″(x)=-6x,当x∈(0,π/ 2 )时,f″(x)<0,故为凸函数,排除C;
故选D.

练习册系列答案
相关题目
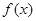 在D上可导,即
在D上可导,即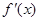 存在,且导函数
存在,且导函数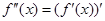 ,若
,若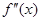 >
0在D上恒成立,则称
>
0在D上恒成立,则称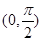 上是凹函数的是(
)
上是凹函数的是(
)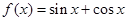 B.
B.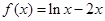
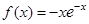 D.
D.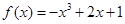
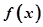 在D上可导,即
在D上可导,即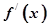 存在,且导函数
存在,且导函数 =
=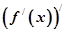 ,若
,若 上不是凸函数的是( )
上不是凸函数的是( ) 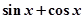 B.
B. 
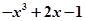 D.
D. 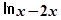
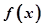 在D上可导,即
在D上可导,即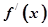 存在,且导函数
存在,且导函数 =
= 。若
。若 上不是凸函数的是( )
上不是凸函数的是( )  B.
B. 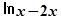
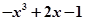 D.
D. 
 在D上可导,即
在D上可导,即 存在,且导函数
存在,且导函数 =
=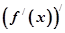 。若
。若 上不是凸函数的是( )
上不是凸函数的是( )  B.
B. 
 D.
D.