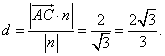题目内容
(08年福建卷文)(本小题满分12分)
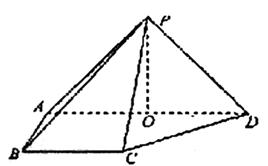
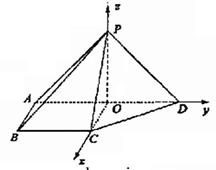
如图,在四棱锥P―ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点A到平面PCD的距离。
解析:(Ⅰ)、本小题主要考查直线与平面的位置关系、异面直线所成角、点到平面的距离等基本知识,考查空间想象能力,逻辑思维能力和运算能力。
解法一:
(Ⅰ)证明:在△PAD卡中PA=PD,O为AD中点,所以PO⊥AD.
又侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,PO![]() 平面PAD,
平面PAD,
所以PO⊥平面ABCD.
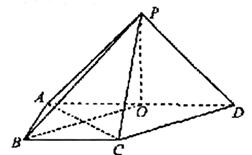
(Ⅱ)连结BO,在直角梯形ABCD中,BC∥AD,AD=2AB=2BC,
有OD∥BC且OD=BC,所以四边形OBCD是平行四边形,
所以OB∥DC.
由(Ⅰ)知PO⊥OB,∠PBO为锐角,
所以∠PBO是异面直线PB与CD所成的角.
因为AD=2AB=2BC=2,在Rt△AOB中,AB=1,AO=1,所以OB=![]() ,
,
在Rt△POA中,因为AP=![]() ,AO=1,所以OP=1,
,AO=1,所以OP=1,
在Rt△PBO中,PB=![]() ,
,
![]() ,
,
所以异面直线PB与CD所成的角的余弦值为![]() .
.
(Ⅲ)由(Ⅱ)得CD=OB=![]() ,
,
在Rt△POC中,PC=![]() ,
,
所以PC=CD=DP,S△PCD=![]() ?2=
?2=![]() 。
。
又![]()
设点A到平面PCD的距离h,
由VP-ACD=VA-PCD,
得![]() S△ACD?OP=
S△ACD?OP=![]() S△PCD?h,
S△PCD?h,
即![]() ×1×1=
×1×1=![]() ×
×![]() ×h,
×h,
解得![]() 。
。
解法二:
(Ⅰ)同解法一,
(Ⅱ)以O为坐标原点,![]() 的方向分别为x轴、y轴、z轴的正方向,
的方向分别为x轴、y轴、z轴的正方向,![]() ,依题意,易得
,依题意,易得![]() ,
,
所以![]()
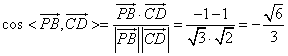 .
.
所以异面直线![]() 与
与![]() 所成的角是
所成的角是![]() .
.
(Ⅲ)设平面![]() 的法向量为
的法向量为![]() .
.
由(Ⅱ)得![]()
则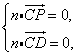 所以
所以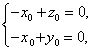 即
即![]() ,
,
取![]() ,得平面
,得平面![]() 的一个法向量为
的一个法向量为![]() .
.
又![]() 。
。
从而点A到平面![]() 的距离
的距离