题目内容
某外商到一开发区投资72万美元建起一座蔬菜加工厂,第一年各种经费支出为12万美元,以后每年都增加4万美元,每年销售蔬菜收入为50万美元.
(1)若扣除投资及各种经费,则从第几年开始获取纯利润?
(2)若干年后,外商为开发新项目,有两种处理方案:
①年平均利润最大时,以48万美元出售该厂;
②纯利润总和最大时,以16万美元出售该厂.
问哪种方案最合算?
答案:
解析:
解析:
|
解:由题设,知每年的经费是以12为首项、4为公差的等差数列. 设纯利润与年数n的关系为f(n),则f(n)=50n-[12n+ (1)要获取利润,就要f(n)>0.所以-2n2+40n-72>0,即n2-20n+36<0.所以2<n<18.因为n∈N*,n=3,4,5,…,17.所以从第3年开始获利. (2)①年平均利润= ②f(n)=-2(n-10)2+128,当n=10时,f(n)最大为128.故方案(2)共获利128+16=144万美元.比较两种方案,获利均为144万美元,但方案(1)只需6年,故选方案(1)最合算. |

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
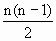 ×4]-72=-2n2+40n-72.
×4]-72=-2n2+40n-72.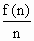 =
=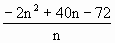 =40-2(n+
=40-2(n+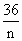 ).因为n+
).因为n+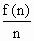 ≤40-2×12=16.所以方案(1)共获利16×6+48=144万美元,此时n=6.
≤40-2×12=16.所以方案(1)共获利16×6+48=144万美元,此时n=6.