题目内容
已知![]() .
.
(Ⅰ)若![]() 在
在![]() 上为增函数,求实数a的取值范围;
上为增函数,求实数a的取值范围;
(Ⅱ)当常数![]() 时,设
时,设![]() ,求
,求![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
解:(Ⅰ)∵![]() 在
在![]() 上为增函数,
上为增函数,
∴![]() 对
对![]() 恒成立. 2分
恒成立. 2分
令![]() ,则
,则![]() 对
对![]() 恒成立,
恒成立,
∴![]() ,解得
,解得![]() ,
,
∴实数![]() 的取值范围是
的取值范围是![]() . ……6分
. ……6分
(Ⅱ)当![]() 时,
时,![]() ,∴
,∴![]() ,…………8分
,…………8分
记![]() ,则
,则![]() 对
对![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上是减函数,∴
上是减函数,∴![]() ,即
,即![]() ,
,
∴当![]() 时,
时,![]() 在
在![]() 上是减函数,得
上是减函数,得![]() 在
在![]() 上为减函数.
上为减函数.
∴当![]() 时,
时,![]() 取得最大值
取得最大值![]() ;当
;当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
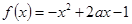 ,若
,若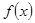 在
在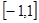 上的最大值为
上的最大值为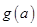 ,求
,求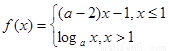 ,若
,若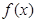 在
在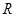 上单调递增,则实数
上单调递增,则实数 的取值范围为为
的取值范围为为

 ,若
,若 在
在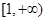 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.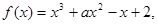
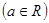
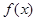 在
在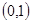 上是减函数,求
上是减函数,求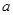 的最大值;
的最大值;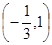 ,求函数y=
,求函数y=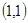 的切线与两坐标轴围成图形的面积。
的切线与两坐标轴围成图形的面积。