题目内容
设函数 的导函数
的导函数 的最大值为3,则
的最大值为3,则 的图象的一条对称轴的方程是( )
的图象的一条对称轴的方程是( )
A. | B. | C. | D. |
A
解析试题分析:对函数求导可得,f′(x)=ωcos(ωx+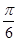 )
)
由导数f′(x)的最大值为3可得ω=3
∴f(x)=sin(3x+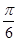 )-1
)-1
由三角函数的性质可得,函数的对称轴处将取得函数的最值结合选项,可得x=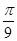
故选A
考点:本题主要考查了函数的求导的基本运算,三角函数的性质:对称轴处取得函数的最值的应用,属于基础试题,试题难度不大.
点评:解决该试题的关键是先对函数求导,由导数f′(x)的最大值为3,可得ω的值,从而可得函数的解析式,然后结合三角函数的性质可得函数的对称轴处取得函数的最值从而可得

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数 的部分图像,则函数的解析式( )
的部分图像,则函数的解析式( )
A. | B. |
C. | D. |
若 ,则
,则 的值为( )
的值为( )
| A.1 | B.-1 | C.0 | D. |
对于函数 给出下列结论:①图象关于原点成中心对称; ②图象关于直线
给出下列结论:①图象关于原点成中心对称; ②图象关于直线 成轴对称;③图象可由函数
成轴对称;③图象可由函数 的图像向左平移
的图像向左平移 个单位得到;④图像向左平移
个单位得到;④图像向左平移 个单位,即得到函数
个单位,即得到函数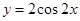 的图像。其中正确结论是 ( );
的图像。其中正确结论是 ( );
| A.①③ | B.②④ | C.②③④ | D.①②③④ |
和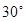 终边在同一条直线上的角的集合是( )
终边在同一条直线上的角的集合是( )
A.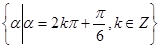 | B.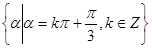 |
C.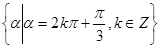 | D.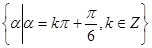 |
若 为第三象限角,且
为第三象限角,且 ,则
,则 为( )
为( )
| A.第一象限角 | B.第二象限角 | C.第三象限角 | D.第四象限角 |
若函数 ,则
,则 是( )
是( )
| A.仅有最小值的奇函数 | B.仅有最大值的偶函数 |
| C.既有最大值又有最小值的偶函数 | D.非奇非偶函数 |
设CD是△ABC的边AB上的高,且满足 ,则( )
,则( )
A. | B. 或 或 |
C. 或 或 | D. 或 或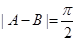 |
 的部分图象如右图,则
的部分图象如右图,则 ,
,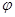 可以取的一组值是( ).
可以取的一组值是( ). 



