题目内容
 如图所示,在正三棱锥A-BCD中,E,F分别为BD,AD的中点,EF⊥CF,则直线BD与平面ACD所成的角为
如图所示,在正三棱锥A-BCD中,E,F分别为BD,AD的中点,EF⊥CF,则直线BD与平面ACD所成的角为分析:设点A在面BCD内的射影为A′,由三棱锥A-BCD为正三棱锥,易得A′为△BCD中心,由线面垂直的判定定理可得AB⊥面ACD,即∠ADB为直线BD与平面ACD所成角,解三角形ADB可得直线BD与平面ACD所成的角.
解答: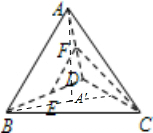 解:设点A在面BCD内的射影为A′
解:设点A在面BCD内的射影为A′
∵三棱锥A-BCD为正三棱锥
∴AB=AD
△BCD为正三角形
A′为△BCD中心
∴CD⊥BA′,
∵AA′⊥面BCD
∴CD⊥AB,
∵E、F分别为BD、AD的中点
∴EF∥AB,
∵EF⊥CF,
∴AB⊥CF
又∵AB⊥CD,CD∩CF=C
∴AB⊥面ACD,
∴AB⊥AD
∠ADB即为直线BD与平面ACD所成角
又∵AB=AD,AB⊥AD,
∴∠ADB=45°
∴直线BD与平面ACD所成角为45°
故答案为:45°
 解:设点A在面BCD内的射影为A′
解:设点A在面BCD内的射影为A′∵三棱锥A-BCD为正三棱锥
∴AB=AD
△BCD为正三角形
A′为△BCD中心
∴CD⊥BA′,
∵AA′⊥面BCD
∴CD⊥AB,
∵E、F分别为BD、AD的中点
∴EF∥AB,
∵EF⊥CF,
∴AB⊥CF
又∵AB⊥CD,CD∩CF=C
∴AB⊥面ACD,
∴AB⊥AD
∠ADB即为直线BD与平面ACD所成角
又∵AB=AD,AB⊥AD,
∴∠ADB=45°
∴直线BD与平面ACD所成角为45°
故答案为:45°
点评:本题考查的知识点是直线与平面所成的角,其中求出∠ADB为直线BD与平面ACD所成角是解答的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
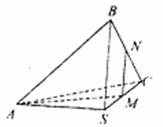
如图所示,在正三棱锥S—ABC中,M、N分别是S
A.BC的中点,且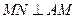 ,若侧棱 ,若侧棱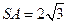 ,则正三棱锥S—ABC外接球的表面积是() ,则正三棱锥S—ABC外接球的表面积是()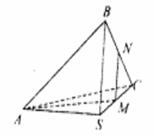 | ||
B.12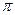 | C.32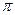 C C .36 .36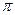 | D.48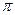  |
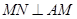 ,若侧棱
,若侧棱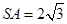 ,则正三棱锥S—ABC外接球的表面积是( )
,则正三棱锥S—ABC外接球的表面积是( )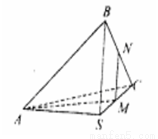
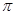 B.32
B.32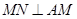 ,若侧棱
,若侧棱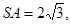 则正三棱锥S—ABC外接球的表面积是 ( )
则正三棱锥S—ABC外接球的表面积是 ( )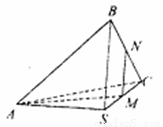
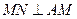 ,
, 若侧棱
若侧棱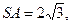 则正三棱锥S—ABC外接球的表面积是 ( )
则正三棱锥S—ABC外接球的表面积是 ( )