题目内容
已知函数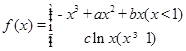 的图像在点
的图像在点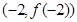 处的切线方程为
处的切线方程为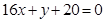 .
.
(Ⅰ)求实数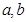 的值;
的值;
(Ⅱ)求函数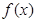 在区间
在区间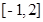 上的最大值;
上的最大值;
(Ⅲ)若曲线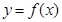 上存在两点
上存在两点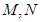 使得
使得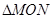 是以坐标原点
是以坐标原点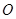 为直角顶点的直角三角形,且斜边
为直角顶点的直角三角形,且斜边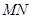 的中点在
的中点在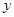 轴上,求实数
轴上,求实数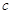 的取值范围.
的取值范围.
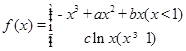 的图像在点
的图像在点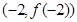 处的切线方程为
处的切线方程为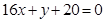 .
.(Ⅰ)求实数
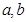 的值;
的值;(Ⅱ)求函数
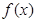 在区间
在区间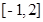 上的最大值;
上的最大值;(Ⅲ)若曲线
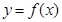 上存在两点
上存在两点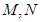 使得
使得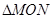 是以坐标原点
是以坐标原点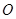 为直角顶点的直角三角形,且斜边
为直角顶点的直角三角形,且斜边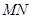 的中点在
的中点在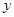 轴上,求实数
轴上,求实数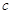 的取值范围.
的取值范围.(Ⅰ) ;(Ⅱ)当
;(Ⅱ)当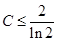 时
时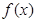 在[-1,2]上的最大值为2,
在[-1,2]上的最大值为2,
当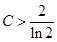 时
时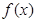 在[-1,2]上的最大值为
在[-1,2]上的最大值为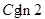 ;(Ⅲ)
;(Ⅲ)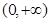 .
.
 ;(Ⅱ)当
;(Ⅱ)当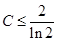 时
时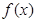 在[-1,2]上的最大值为2,
在[-1,2]上的最大值为2,当
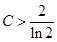 时
时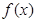 在[-1,2]上的最大值为
在[-1,2]上的最大值为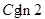 ;(Ⅲ)
;(Ⅲ)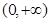 .
.试题分析:(Ⅰ)由题意先对
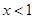 时的函数
时的函数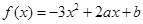 进行求导,易得
进行求导,易得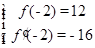 ,解得
,解得 ;(Ⅱ)因为函数
;(Ⅱ)因为函数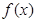 为分段函数,要求在区间
为分段函数,要求在区间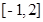 上的最大值,需分别求区间
上的最大值,需分别求区间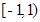 和
和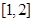 上的最大值,当
上的最大值,当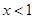 时,应对函数
时,应对函数 进行求导,求函数的单调性,从而求区间
进行求导,求函数的单调性,从而求区间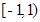 上的最大值;当
上的最大值;当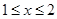 时,应对函数
时,应对函数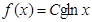 分
分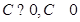 两种情况讨论,可得结论;(Ⅲ)根据条件可知
两种情况讨论,可得结论;(Ⅲ)根据条件可知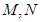 的横坐标互为相反数,不妨设
的横坐标互为相反数,不妨设
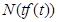 ,其中
,其中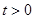 ,若
,若 ,则
,则 ,由
,由 是直角,得
是直角,得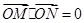 ,即
,即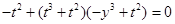 ,方程无解;若
,方程无解;若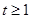 ,则
,则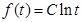 由于
由于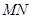 中的中点在
中的中点在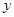 轴上,且
轴上,且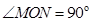 ,所以
,所以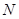 点不可能在
点不可能在 轴上,即
轴上,即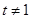 同理有
同理有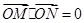 ,
,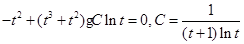 ,得
,得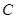 的范围是
的范围是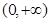 .
.试题解析:(I)当
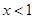 时
时 ,
,因为函数图象在点
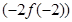 处的切线方程为
处的切线方程为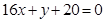 ,
,所以切点坐标为
 且
且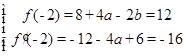 解得
解得 . 4分
. 4分(II)由(I)得,当
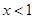 时
时 ,令
,令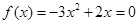 ,
,可得
 或
或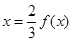 在
在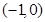 和
和 上单调递减,在
上单调递减,在 上单调递增,所以在
上单调递增,所以在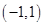 上
上 的最大值为
的最大值为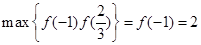 ,当
,当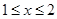 时,
时,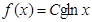 ,
,当
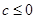 时,
时,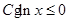 恒成立
恒成立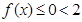 此时
此时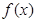 在[-1,2]上的最大值为
在[-1,2]上的最大值为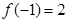 ;
;当
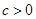 时
时 在[1,2]上单调递增,且
在[1,2]上单调递增,且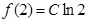 ,
,令
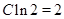 则
则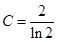 ,
,所以当
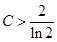 时
时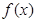 在[-1,2]上的最大值为
在[-1,2]上的最大值为 ,
,当
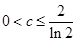 时
时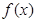 在[-1,2]上的最大值为
在[-1,2]上的最大值为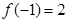 ,
,综上可知,当
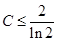 时
时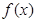 在[-1,2]上的最大值为2,
在[-1,2]上的最大值为2,时当
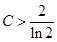 时
时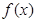 在[-1,2]上的最大值为
在[-1,2]上的最大值为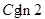 . 9分
. 9分(III)
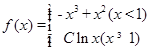 根据条件可知
根据条件可知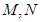 的横坐标互为相反数,
的横坐标互为相反数,不妨设

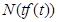 ,其中
,其中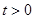 ,
,若
 ,则
,则 ,由
,由 是直角,得
是直角,得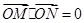 ,即
,即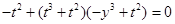 ,
,即
 此方程无解;
此方程无解;若
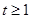 ,则
,则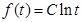 由于
由于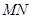 中的中点在
中的中点在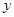 轴上,且
轴上,且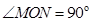 ,所以
,所以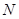 点不可能在
点不可能在 轴上,
轴上,即
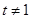 同理有
同理有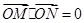 ,
,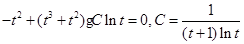 ,
,令
 由于函数
由于函数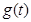 的值域是
的值域是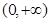
所以实数
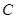 的取值范围是
的取值范围是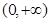 14分
14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
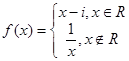 ,则
,则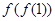 在复平面内对应的点位于( )
在复平面内对应的点位于( ) ,设
,设
 ,若
,若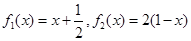 ,则f(x)的最大值为( )
,则f(x)的最大值为( )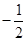

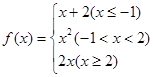 ,若
,若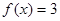 ,则x的值是 ( )
,则x的值是 ( ) 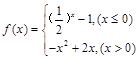 ,对于下列命题:
,对于下列命题: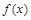 的最小值是0;
的最小值是0;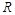 上是单调递减函数;
上是单调递减函数;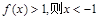 ;
;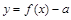 有三个零点,则
有三个零点,则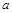 的取值范围是
的取值范围是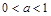 ;
;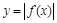 关于直线
关于直线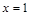 对称.
对称.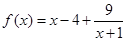 ,
,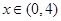 ,当
,当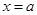 时,
时,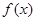 取得最小值
取得最小值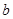 ,则在直角坐标系中函数
,则在直角坐标系中函数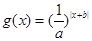 的图像为( )
的图像为( )
 是
是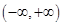 上的增函数,则实数
上的增函数,则实数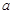 的取值范围是( )
的取值范围是( )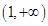
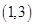
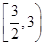
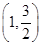
 ,则
,则 .
.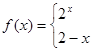
 ,则
,则 .
.