题目内容
已知平面坐标系中,点O为原点,A(-3,-4),B(5,-12)(1)若
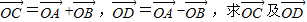 的坐标;
的坐标;(2)求
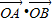 ;
;(3)若点P在直线AB上,且
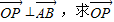 的坐标.
的坐标.
【答案】分析:(1)先由题设条件得到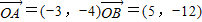 ,再将两向量用
,再将两向量用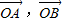 两个向量表示出来,从而求得两向量的坐标;
两个向量表示出来,从而求得两向量的坐标;
(2)由向量的数量积坐标表示求出两向量的数量积.
(3)设P(m,n)由P在AB上,得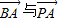 共线由此求得m,n的关系,再由两向量
共线由此求得m,n的关系,再由两向量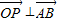 ,得到关于m,n的另一个方程,将此两方程联立求得m,n,即可得到点P的坐标,亦即得到向量
,得到关于m,n的另一个方程,将此两方程联立求得m,n,即可得到点P的坐标,亦即得到向量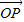 的坐标.
的坐标.
解答:解:(1)∵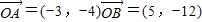
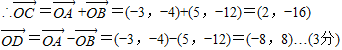
(2)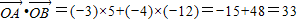
(3)设P(m,n)
∵P在AB上,
∴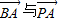 共线
共线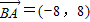

∴(-8)•(-4-n)-8(-3-m)=0
即m+n=-7①又∵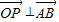 ∴(m,n)•(8,-8)=0
∴(m,n)•(8,-8)=0
那m-n=0②由①②解得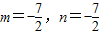 即
即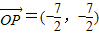
点评:本题考查了两向量垂直的条件,共线的条件,数量积的运算,涉及到的知识点较多,解题的关键是熟练掌握向量相关基本知识与基本用法,本题考查了转化的思想及方程思想
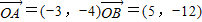 ,再将两向量用
,再将两向量用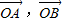 两个向量表示出来,从而求得两向量的坐标;
两个向量表示出来,从而求得两向量的坐标;(2)由向量的数量积坐标表示求出两向量的数量积.
(3)设P(m,n)由P在AB上,得
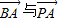 共线由此求得m,n的关系,再由两向量
共线由此求得m,n的关系,再由两向量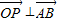 ,得到关于m,n的另一个方程,将此两方程联立求得m,n,即可得到点P的坐标,亦即得到向量
,得到关于m,n的另一个方程,将此两方程联立求得m,n,即可得到点P的坐标,亦即得到向量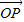 的坐标.
的坐标.解答:解:(1)∵
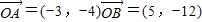
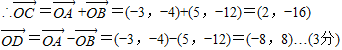
(2)
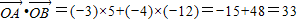
(3)设P(m,n)
∵P在AB上,
∴
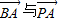 共线
共线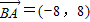

∴(-8)•(-4-n)-8(-3-m)=0
即m+n=-7①又∵
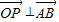 ∴(m,n)•(8,-8)=0
∴(m,n)•(8,-8)=0那m-n=0②由①②解得
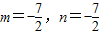 即
即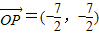
点评:本题考查了两向量垂直的条件,共线的条件,数量积的运算,涉及到的知识点较多,解题的关键是熟练掌握向量相关基本知识与基本用法,本题考查了转化的思想及方程思想

练习册系列答案
相关题目