题目内容
16.设Sn为数列{an}的前n项和,若Sn=5an-1,则an=$\frac{1}{4}×(\frac{5}{4})^{n-1}$.分析 由已知的数列递推式求出首项,再由数列递推式得到数列{an}是以$\frac{1}{4}$为首项,以$\frac{5}{4}$为公比的等比数列.则an可求.
解答 解:由Sn=5an-1,取n=1,得a1=5a1-1,∴${a}_{1}=\frac{1}{4}$;
当n≥2时,an=Sn-Sn-1=5an-1-5an-1+1,
∴4an=5an-1,即$\frac{{a}_{n}}{{a}_{n-1}}=\frac{5}{4}$(n≥2).
则数列{an}是以$\frac{1}{4}$为首项,以$\frac{5}{4}$为公比的等比数列.
∴${a}_{n}=\frac{1}{4}×(\frac{5}{4})^{n-1}$.
故答案为:$\frac{1}{4}×(\frac{5}{4})^{n-1}$.
点评 本题考查了递推关系的应用、等比数列的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.如图所示,三视图表示的几何体是( )
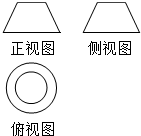

| A. | 圆台 | B. | 棱台 | C. | 棱柱 | D. | 圆锥 |
4.如图是函数f(x)=Acos($\frac{2}{3}$πx+φ)-1(A>0,|φ|<$\frac{π}{2}$)的图象的一部分,则f(2015)=( )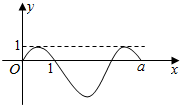

| A. | 1 | B. | 2 | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -3 |
1.设集合A{x|x∈N},且1≤x≤26,B={a,b,c,…,z},对应关系f:A→B如表(即1到26按由小到大顺序排列的自然数与按照字母表顺序排列的26个英文小写字母之间的一一对应):
又知函数g(x)=$\left\{\begin{array}{l}{lo{g}_{2}(32-x)(22<x<32)}\\{x+4(0≤x≤22)}\end{array}\right.$,若f[g(x1)],f[g(20)],f[g(x2)],f[g(9)]所表示的字母依次排列恰好组成的英文单词为“exam”,则x1+x2=31.
| x | 1 | 2 | 3 | 4 | 5 | … | 25 | 26 |
| f(x) | a | b | c | d | e | … | y | z |
8.已知集合M={-2,-1,0,1},N={x|$\frac{1}{2}$≤2x≤4},x∈Z},则M∩N=( )
| A. | M={-2,-1,0,1,2} | B. | M={-1,0,1,2} | C. | M={-1,0,1} | D. | M={0,1} |