题目内容
讨论函数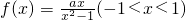
的单调性并证明．
证明：设-1＜x1＜x2＜1，
则
=
，
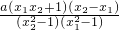∵-1＜x1＜x2＜1，
∴x1x2+1＞0，x2-x1＞0，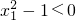
，
，
∴
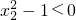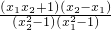＞0，
∴当a＞0时，f（x1）＞f（x2），∴f（x）在（-1，1）是减函数，
当a＜0时，f（x1）＜f（x2），∴f（x）在（-1，1）上是增函数，
当a=0时，f（x）=0，∴f（x）在（-1，1）上不具有单调性．
分析：先在定义域上取值，再作差、变形，变形彻底后根据式子的特点，对a进行分类讨论判断符号、下结论．
点评：本题考查了函数单调性的证明方法：定义法，关键是变形一定彻底，直到能明显的判断出符号为止．
则
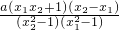=，∵-1＜x1＜x2＜1，
∴x1x2+1＞0，x2-x1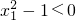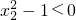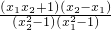＞0，
，，∴
＞0，∴当a＞0时，f（x1）＞f（x2），∴f（x）在（-1，1）是减函数，
当a＜0时，f（x1）＜f（x2），∴f（x）在（-1，1）上是增函数，
当a=0时，f（x）=0，∴f（x）在（-1，1）上不具有单调性．
分析：先在定义域上取值，再作差、变形，变形彻底后根据式子的特点，对a进行分类讨论判断符号、下结论．
点评：本题考查了函数单调性的证明方法：定义法，关键是变形一定彻底，直到能明显的判断出符号为止．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目