题目内容
以椭圆
的焦点为顶点，离心率为
的双曲线方程（ ）
A． | B． |
| C．或 | D．以上都不对 |
B
解析知识点：椭圆焦点，双曲线方程的求法，离心率
解：椭圆
的焦点为（3，0）和（-3,0）由题意知道双曲线的顶点坐标为（3,0）
（-3,0）所以a=3.由双曲线的离心率e=2，得
，解得c=6，
双曲线方程为
，选B.
点评：此题要熟练掌握椭圆，双曲线的顶点，焦点的计算。
练习册系列答案
阅读快车系列答案
相关题目
抛物线
的焦点坐标是：
| A．（0，-1） | B．（0,1） | C．（1,0） （ | D．（-1,0） |
，其中
为2,4,6,8中任取的一个数，
为1,3,5,7中任取的一个数，从这些抛物线中任意抽取两条，它们在与直线
交点处的切线相互平行的概率是（ ）
设椭圆
，右焦点F（c,0），方程
的两个根分别为x1,x2，则点P（x1,x2）在 （ ）
A．圆 上 | B．圆内 |
| C．圆外 | D．以上三种情况都有可能 |
面
的斜线 AB 交于点 B，过定点 A 的动直线
与 AB 垂直，且交于点C，则动点C的轨迹是
| A．一条直线 | B．一个圆 | C．一个椭圆 | D．双曲线的一支 |
（普通高中做）抛物线
的焦点坐标是
A． | B． | C． | D． |
已知椭圆
，以椭圆的焦点为顶点，顶点为焦点的双曲线方程是
A． | B． | C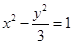． | D． |
抛物线
上的点P到直线y=2x+4有最短的距离，则P的坐标是（ ）
A．（ ， ） | B．(0，0) | C．（2 ，2） | D． |
直线
与椭圆
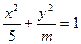恒有公共点。则实数m的取值范围是（ ）
| A．（0，1） | B．（0，5） | C． | D．（1， |