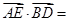题目内容
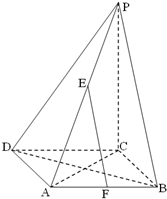 如图,在边长为2的菱形ABCD中,∠ABC=60°,PC⊥面ABCD,E,F是PA和AB的中点.
如图,在边长为2的菱形ABCD中,∠ABC=60°,PC⊥面ABCD,E,F是PA和AB的中点.(Ⅰ)求证:EF∥平面PBC;
(Ⅱ)若PC=2,求PA与平面PBC所成角的正弦值.
分析:(I)欲证EF∥平面PBC,根据直线与平面平行的判定定理可知只需证EF与平面PBC内一直线平行,而EF∥PB,又EF?平面PBC,PB?平面PBC,满足定理所需条件;
(II)过A作AH⊥BC于H,连接PH,则∠APH为PA与平面PBC所成的角,利用sin∠APH=
,可得结论.
(II)过A作AH⊥BC于H,连接PH,则∠APH为PA与平面PBC所成的角,利用sin∠APH=
| AH |
| PA |
解答: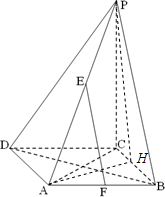 (I)证明:∵E,F是PA和AB的中点,
(I)证明:∵E,F是PA和AB的中点,
∴AE=PE,AF=BF,
∴EF∥PB
又EF?平面PBC,PB?平面PBC,
故EF∥平面PBC;
(II)解:过A作AH⊥BC于H,连接PH
∵PC⊥面ABCD,AH?面ABCD,
∴PC⊥AH
∵PC∩BC=C
∴AH⊥平面PBC
∴∠APH为PA与平面PBC所成的角
∵边长为2的菱形ABCD中,∠ABC=60°,
∴△ABC为正三角形
∵AH⊥BC
∴H为BC的中点,AH=
∵PC=AC=2,∴PA=2
∴sin∠APH=
=
∴PA与平面PBC所成角的正弦值为
.
 (I)证明:∵E,F是PA和AB的中点,
(I)证明:∵E,F是PA和AB的中点,∴AE=PE,AF=BF,
∴EF∥PB
又EF?平面PBC,PB?平面PBC,
故EF∥平面PBC;
(II)解:过A作AH⊥BC于H,连接PH
∵PC⊥面ABCD,AH?面ABCD,
∴PC⊥AH
∵PC∩BC=C
∴AH⊥平面PBC
∴∠APH为PA与平面PBC所成的角
∵边长为2的菱形ABCD中,∠ABC=60°,
∴△ABC为正三角形
∵AH⊥BC
∴H为BC的中点,AH=
| 3 |
∵PC=AC=2,∴PA=2
| 2 |
∴sin∠APH=
| AH |
| PA |
| ||
| 4 |
∴PA与平面PBC所成角的正弦值为
| ||
| 4 |
点评:本题主要考查了直线与平面平行的判定,考查线面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
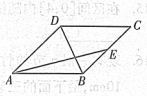
 (2013•昌平区二模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为CD的中点,则
(2013•昌平区二模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为CD的中点,则 (2013•潍坊一模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为BC中点,则
(2013•潍坊一模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为BC中点,则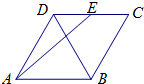 (2013•昌平区二模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为CD的中点,则
(2013•昌平区二模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为CD的中点,则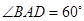 , E为BC中点,则
, E为BC中点,则