题目内容
等轴双曲线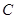 的中心在原点,焦点在
的中心在原点,焦点在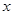 轴上,
轴上,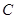 与抛物线
与抛物线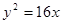 的准线交于
的准线交于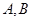 两点,
两点, ;则
;则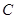 的实轴长为____________.
的实轴长为____________.
【答案】

【解析】
试题分析:设等轴双曲线C:x2-y2=a2(a>0),
y2=16x的准线l:x=-4,
∵C与抛物线y2=16x的准线l:x=-4交于A,B两点,|AB|=4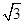
∴A(-4,2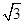 ),B(-4,-2
),B(-4,-2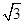 ),
),
将A点坐标代入双曲线方程得a2=(-4)2-(2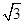 )2=4,
)2=4,
∴a=2,2a=4.答案为4.
考点:本题主要考查抛物线的标准方程,双曲线的几何性质。
点评:基础题,本题给出等轴双曲线,在已知双曲线被抛物线的准线截得线段长的情况下求双曲线的实轴长,体现综合性.

练习册系列答案
相关题目
 的中心在原点,焦点在
的中心在原点,焦点在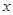 轴上,
轴上,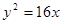 的准线交于
的准线交于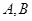 两点,
两点,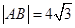 ,则
,则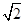 B.
B.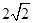 C.
C.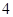 D.
D.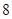
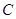 的中心在原点,焦点在
的中心在原点,焦点在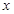 轴上,
轴上, 的准线交于
的准线交于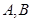 两点,
两点,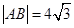 ;则
;则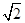 B.
B.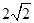 C.
C.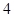 D.
D.