题目内容
(本小题12分)
在平面直角坐标系 中,直线
中,直线 与抛物线
与抛物线 相交于
相交于 .
. 两点。
两点。
(1)求证:“如果直线 过点
过点 ,那么
,那么 ”是真命题。
”是真命题。
(2)写出(1)中命题的逆命题(直线 与抛物线
与抛物线 相交于
相交于 .
. 两点为大前提),判断它是真命题还是假命题,如果是真命题,写出证明过程;如果是假命题,举出反例说明
两点为大前提),判断它是真命题还是假命题,如果是真命题,写出证明过程;如果是假命题,举出反例说明
【答案】
证明:(1)设过点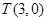 的直线
的直线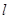 交抛物线
交抛物线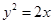 于点
于点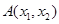 ,
,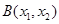 ,
,
当直线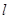 的斜率不存在时,直线
的斜率不存在时,直线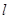 的方程为
的方程为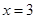 ,此时,直线
,此时,直线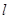 与抛物线相交于
与抛物线相交于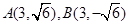 ,
,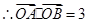 。----------------2分
。----------------2分
当直线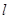 的斜率存在时,设直线
的斜率存在时,设直线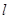 的方程为
的方程为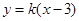 ,其中
,其中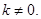
由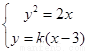 得
得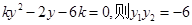 -------------------4分
-------------------4分
又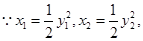
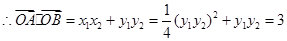
综上,“直线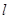 与抛物线
与抛物线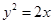 相交于
相交于 .
.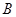 两点,如果直线
两点,如果直线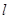 过点
过点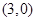 ,那么
,那么 ”是真命题。---------------------6分(注,如果设
”是真命题。---------------------6分(注,如果设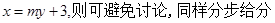 )
)
(2) (1)中命题的逆命题是:“直线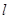 交抛物线
交抛物线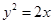 于
于 .
.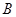 两点,如果
两点,如果 ,那么直线
,那么直线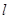 过点
过点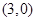 ”--------------------8分
”--------------------8分
该命题是个假命题。-----------------------9分
例如:取抛物线上的点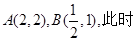
 ,直线AB的方程为
,直线AB的方程为 ,而点(3,0)不在直线AB上。--------------------12分
,而点(3,0)不在直线AB上。--------------------12分
【解析】略

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目

 ,且△ABC的面积为
,且△ABC的面积为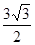
 ,求a+b的值。
,求a+b的值。 ABC中,设
ABC中,设 ,求A的值。
,求A的值。