题目内容
已知函数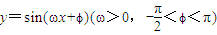 为偶函数,在函数的一个周期内,点A,B分别为函数的最低点和最高点,且
为偶函数,在函数的一个周期内,点A,B分别为函数的最低点和最高点,且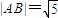 ,则ω,ϕ的值分别为( )
,则ω,ϕ的值分别为( )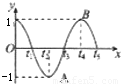
A.2π,0
B.π,
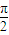
C.
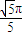 ,0
,0D.π,0
【答案】分析:由函数的图象可得函数为偶函数,结合ϕ的范围求得ϕ=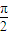 ,设函数的周期为T,由|AB|=
,设函数的周期为T,由|AB|=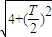 =
=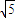 ,解得T的值,
,解得T的值,
再由T=2=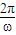 求得ω 的值.
求得ω 的值.
解答:解: ∵函数y=sin(ωx+ϕ)(ω>0,0<ϕ<π)为偶函数,∴ϕ=
∵函数y=sin(ωx+ϕ)(ω>0,0<ϕ<π)为偶函数,∴ϕ=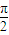 ,
,
∵A,B两点间距离为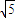 ,设函数的周期为T,
,设函数的周期为T,
则由|AB|=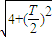 =
=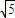 ,解得T=2,即
,解得T=2,即 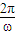 =2,ω=π.
=2,ω=π.
故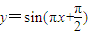 .
.
故选B.
点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求函数的解析式,余弦函数的对称性,属于中档题.
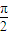 ,设函数的周期为T,由|AB|=
,设函数的周期为T,由|AB|=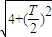 =
=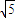 ,解得T的值,
,解得T的值,再由T=2=
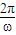 求得ω 的值.
求得ω 的值.解答:解:
 ∵函数y=sin(ωx+ϕ)(ω>0,0<ϕ<π)为偶函数,∴ϕ=
∵函数y=sin(ωx+ϕ)(ω>0,0<ϕ<π)为偶函数,∴ϕ=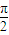 ,
,∵A,B两点间距离为
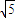 ,设函数的周期为T,
,设函数的周期为T,则由|AB|=
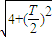 =
=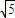 ,解得T=2,即
,解得T=2,即 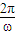 =2,ω=π.
=2,ω=π.故
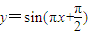 .
.故选B.
点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求函数的解析式,余弦函数的对称性,属于中档题.

练习册系列答案
相关题目
 为偶函数,且
为偶函数,且 在
在 上递减,设
上递减,设 ,
, ,
, ,则
,则 的大小关系正确的是( )
的大小关系正确的是( ) (B)
(B) (C)
(C) (D)
(D)
 为偶函数,且在
为偶函数,且在 上为增函数.
上为增函数. 的值,并确定
的值,并确定 的解析式;
的解析式; 且
且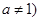 ,是否存在实数
,是否存在实数 使
使 在区间
在区间 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.