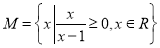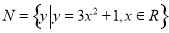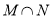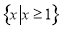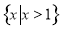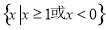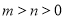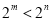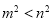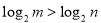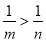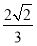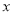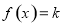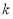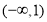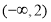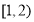题目内容
已知函数 ,
,
(1)求该函数的定义域和值域;(2)判断函数的奇偶性,并加以证明。
(1) 定义域为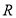 ,值域为
,值域为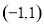 ;(2)
;(2) 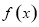 为奇函数.
为奇函数.
【解析】
试题分析:(1)求函数定义域使函数有意义即分母不为0,求值域方法有多种,①由函数单调性求值, ②由常见函数值域求值域,③反函数法求值域,④配方法求值域,⑤分离常数法⑥换元法等等.(2) 首先求出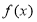 的定义域关于原点对称,然后求
的定义域关于原点对称,然后求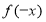 与
与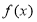 关系由函数奇偶性的定义
关系由函数奇偶性的定义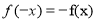 判断
判断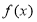 是奇函数;
是奇函数;
试题解析:
(1)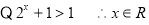
所以定义域为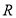
记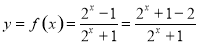
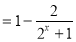
由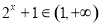 知
知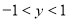
 值域为
值域为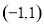
(2) 为奇函数
为奇函数
事实上,定义域为R,关于原点对称,
且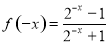

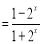
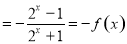
故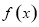 为奇函数
为奇函数
考点:函数奇偶性的判断;函数的值域.

练习册系列答案
相关题目