题目内容
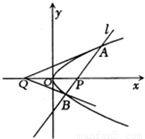
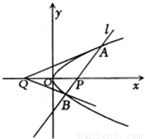
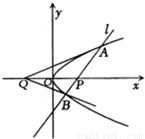
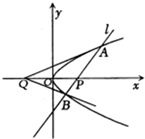 已知不垂直于x轴的动直线l交抛物线y2=2mx(m>0)于A、B两点,若A、B两点满足∠AQP=∠BQP,其中Q(-4,0),原点O为PQ的中点.
已知不垂直于x轴的动直线l交抛物线y2=2mx(m>0)于A、B两点,若A、B两点满足∠AQP=∠BQP,其中Q(-4,0),原点O为PQ的中点.①求证:A、P、B三点共线;
②当m=2时,是否存在垂直于x轴的直线l′,使得l′被以AP为直径的圆所截得的弦长为定值,如果存在,求出l′的方程,如果不存在,请说明理由.
分析:①先根据∵∠AQP=∠BQP且显然是锐角得到tan∠AQP=tan∠BQP.即KAQ=-kBQ,从而得到点A,B之间的关系,再求出直线AP与PB的斜率即可证明结论;
②设出直线方程以及点A的坐标和以AP为直径的圆心C圆心坐标;再求出对应弦长,即可求出结论.
②设出直线方程以及点A的坐标和以AP为直径的圆心C圆心坐标;再求出对应弦长,即可求出结论.
解答:解:①证明:由题意可设A(
,y1):B(
,y2),P(4,0).
∵∠AQP=∠BQP且显然是锐角
∴tan∠AQP=tan∠BQP.即KAQ=-kBQ,
即
=-
?y1y2(y1+y2)=-8m(y1+y2).
∵L不垂直于x轴,
∴y1+y2≠0,y1y2=-8m.
∴kAP=
=
=
=
,
∵kBP=
=
=kAP
∴A,P,B三点共线.
②假设满足题意l′的存在,设l′:x=n,A(x1,y1),则y12=4x1,
∴以AP为直径的圆心C(
,
),
则l′被圆C截得的弦长=2
=2
.
当n=3时,弦长为定值2
.
故存在满足题意的直线l′:x=3.
| y12 |
| 2m |
| y22 |
| 2m |
∵∠AQP=∠BQP且显然是锐角
∴tan∠AQP=tan∠BQP.即KAQ=-kBQ,
即
| y1 | ||
|
| y2 | ||
|
∵L不垂直于x轴,
∴y1+y2≠0,y1y2=-8m.
∴kAP=
| y1 | ||
|
| 2my1 |
| y12-8m |
-2m•
| ||
|
| 2my2 |
| y22-8m |
∵kBP=
| y2 | ||
|
| 2my2 |
| y22-8m |
∴A,P,B三点共线.
②假设满足题意l′的存在,设l′:x=n,A(x1,y1),则y12=4x1,
∴以AP为直径的圆心C(
| x1+4 |
| 2 |
| y1 |
| 2 |
则l′被圆C截得的弦长=2
|
| (n-3)x1+4n-n2 |
当n=3时,弦长为定值2
| 3 |
故存在满足题意的直线l′:x=3.
点评:本题主要考查直线与圆锥曲线的综合问题.直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等 突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法,要求考生分析问题和解决问题的能力、计算能力较高

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
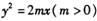 于A、B两点,若A,B两点满足
于A、B两点,若A,B两点满足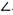 AQP=
AQP=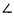 BQP,其中Q(-4,0),原点O为PQ的中点.
BQP,其中Q(-4,0),原点O为PQ的中点.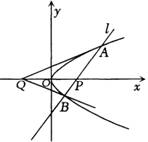
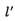 ,使得
,使得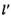 被以为直径的圆所截得的弦长为定值,如果存在,求出
被以为直径的圆所截得的弦长为定值,如果存在,求出