题目内容
【题目】若直角坐标平面内两点P,Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙伴点组”).则下列函数中,恰有两个“伙伴点组”的函数是(填空写所有正确选项的序号)
①y= ![]() ;②y=
;②y=  ;③y=
;③y= ![]() ;④y=
;④y=  .
.
【答案】②③
【解析】解:①函数y=﹣x﹣1,(x<0)关于原点对称的函数为﹣y=x﹣1,即y=﹣x+1,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数只有一个,所以函数f(x)的“伙伴点组”有1个,不满足条件.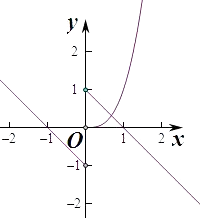
②函数y=﹣ln|x|(x<0)关于原点对称的函数为﹣y=﹣ln|﹣x|,即y=ln|x|,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有2个,所以函数f(x)的“伙伴点组”有2个,满足条件.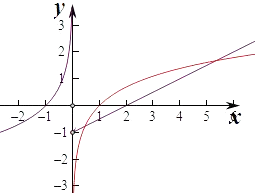
③函数y=﹣x2﹣4x,(x<0)关于原点对称的函数为﹣y=﹣x2+4x,即y=x2﹣4x,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有2个,所以函数f(x)的“伙伴点组”有2个,满足条件.
④函数y=e﹣x , (x<0)关于原点对称的函数为﹣y=ex , 即y=﹣ex ,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有0个,所以函数f(x)的“伙伴点组”有0个,不满足条件.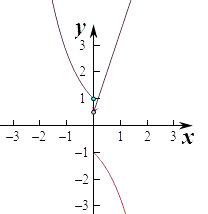 ,
,
所以答案是:②③.
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.

练习册系列答案
相关题目

