题目内容
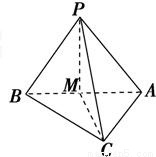
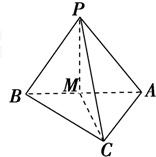如图，已知△ABC为直角三角形，其中∠ACB=90°，M为AB中点，PM垂直于△ABC所在平面，那么
- A.PA=PB＞PC
- B.PA=PB＜PC
- C.PA=PB=PC
- D.PA≠PB≠PC
C
分析：在下底面内找出MA=MB=MC，再利用射影长相等斜线段相等就可选答案．
解答：∵M是Rt△ABC斜边AB的中点，
∴MA=MB=MC．
又∵PM⊥平面ABC，
∴MA、MB、MC分别是PA、PB、PC在平面ABC上的射影，
∴PA=PB=PC．
应选C．
点评：本题考查从同一点出发的斜线段与对应射影长之间的关系，是对线面垂直性质的应用，是基础题．
分析：在下底面内找出MA=MB=MC，再利用射影长相等斜线段相等就可选答案．
解答：∵M是Rt△ABC斜边AB的中点，
∴MA=MB=MC．
又∵PM⊥平面ABC，
∴MA、MB、MC分别是PA、PB、PC在平面ABC上的射影，
∴PA=PB=PC．
应选C．
点评：本题考查从同一点出发的斜线段与对应射影长之间的关系，是对线面垂直性质的应用，是基础题．
练习册系列答案
相关题目
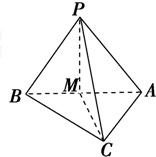10、如图，已知△ABC为直角三角形，其中∠ACB=90°，M为AB中点，PM垂直于△ABC所在平面，那么（ ）
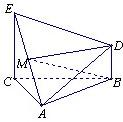如图，已知△ABC为正三角形，EC⊥平面ABC，BD⊥平面ABC，且EC、BD在平面ABC的同侧，M为EA的中点，CE=CA=2BD，求证：
如图：已知△ABC为直角三角形，分别以直角边AC、BC为直径作半圆AmC和BnC，以AB为直径作半圆ACB，记两个月牙形阴影部分的面积之和为S1，△ABC的面积为S2，则S1与S2的大小关系为（ ）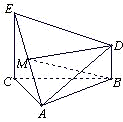
如图，已知△ABC为正三角形，EC⊥平面ABC，BD⊥平面ABC，且EC、BD在平面ABC的同侧，M为EA的中点，CE=CA=2BD，